
某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足f(n)=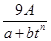 ,其中
,其中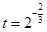 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
(1)栽种9年后,该树木的高度是栽种时高度的8倍;(2)第5年的增长高度最大.
解析试题分析:(1)由题中所给条件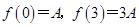 ,运用待定系数法不难求出
,运用待定系数法不难求出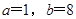 ,进而确定出函数
,进而确定出函数 ,其中
,其中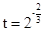 .由
.由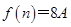 ,运用解方程的方法即可求出
,运用解方程的方法即可求出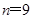 ,问题得解; (2)由前面(1)中已求得
,问题得解; (2)由前面(1)中已求得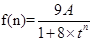 ,可表示出第n年的增长高度为
,可表示出第n年的增长高度为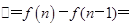
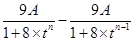 ,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得:
,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得: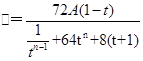 ,观察此式特征能用基本不等式的方法进行求它的最值,即:
,观察此式特征能用基本不等式的方法进行求它的最值,即: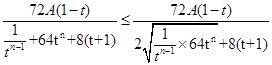 ,成立的条件为 当且仅当
,成立的条件为 当且仅当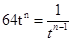 时取等号,即可求出
时取等号,即可求出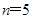 .
.
试题解析: (1)由题意知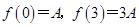 .
.
所以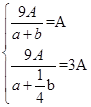 解得
解得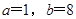 . 4分
. 4分
所以 ,其中
,其中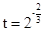 .
.
令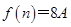 ,得
,得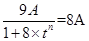 ,解得
,解得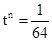 ,
,
所以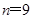 .
.
所以栽种9年后,该树木的高度是栽种时高度的8倍. 6分
(2)由(1)知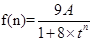 .
.
第n年的增长高度为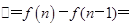
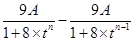 . 9分
. 9分
所以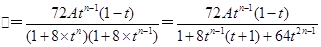
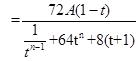 12分
12分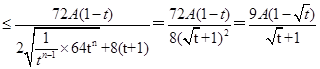 .
.
当且仅当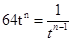 ,即
,即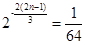 时取等号,此时
时取等号,此时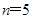 .
.
所以该树木栽种后第5年的增长高度最大. 14分
考点:1.待定系数法求解;2.函数的最值;3.基本不等式的运用


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
已知定义在区间(0,+∞)上的函数f(x)满足f(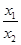 )=f(x1)-f(x2),且当x>1时,f(x)<0.
)=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=log3(9x)·log3(3x), ≤x≤9.
≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆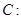
 的左焦点为
的左焦点为 ,左、右顶点分别为
,左、右顶点分别为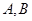 ,过点
,过点 且倾斜角为
且倾斜角为 的直线
的直线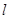 交椭圆于
交椭圆于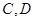 两点,椭圆
两点,椭圆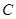 的离心率为
的离心率为 ,
, .
.
(1)求椭圆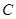 的方程;
的方程;
(2)若 是椭圆上不同两点,
是椭圆上不同两点,
 轴,圆
轴,圆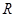 过点
过点 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆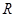 内,则称圆
内,则称圆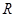 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆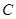 是否存在过点
是否存在过点 的内切圆?若存在,求出点
的内切圆?若存在,求出点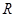 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数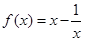 .
.
(1)判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数 在区间
在区间 上为增函数;
上为增函数;
(3)若函数 在区间
在区间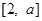 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于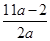 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
(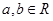 ),其图像在
),其图像在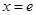 处的切线方程为
处的切线方程为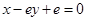 .函数
.函数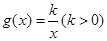 ,
, .
.
(1)求实数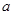 、
、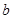 的值;
的值;
(2)以函数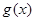 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆 ,若圆
,若圆 上存在两个不同的点到原点
上存在两个不同的点到原点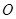 的距离为1,求
的距离为1,求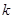 的取值范围;
的取值范围;
(3)求最大的正整数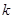 ,对于任意的
,对于任意的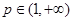 ,存在实数
,存在实数 、
、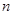 满足
满足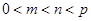 ,使得
,使得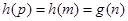 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com