
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,圆
,圆![]() :
:![]() 过椭圆
过椭圆![]() 的三个顶点,过点
的三个顶点,过点![]() 的直线
的直线![]() (斜率存在且不为0)与椭圆
(斜率存在且不为0)与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)证明:在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值,并求出定点
为定值,并求出定点![]() 的坐标.
的坐标.
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①直线![]() 平行于平面
平行于平面![]() 内的一条直线,则
内的一条直线,则![]() ;
;
②若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ;
;
④当![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
的取值范围为![]() .
.
其中正确命题的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
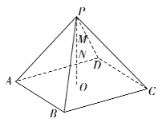
【题目】如图,在四棱锥![]() 中,顶点P在底面的投影
中,顶点P在底面的投影![]() 恰为正方形ABCD的中心且
恰为正方形ABCD的中心且![]() ,设点M,N分别为线段PD,PO上的动点,已知当
,设点M,N分别为线段PD,PO上的动点,已知当![]() 取得最小值时,动点M恰为PD的中点,则该四棱锥的外接球的表面积为____________.
取得最小值时,动点M恰为PD的中点,则该四棱锥的外接球的表面积为____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且![]() .
.
(1)求椭圆C的方程.
(2)不经过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长与椭圆C的长轴长相等,且直线
截得的弦长与椭圆C的长轴长相等,且直线![]() 与椭圆C交于D,E两点,试判断
与椭圆C交于D,E两点,试判断![]() 的周长是否为定值?若是,求出定值;若不是,请说明理由.
的周长是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“非洲猪瘟”过后,全国生猪价格逐步上涨,某大型养猪企业,欲将达到养殖周期的生猪全部出售,根据去年的销售记录,得到销售生猪的重量的频率分布直方图(如图所示).

(1)根据去年生猪重量的频率分布直方图,估计今年生猪出栏(达到养殖周期)时,生猪重量达不到270斤的概率(以频率代替概率);
(2)若假设该企业今年达到养殖周期的生猪出栏量为5000头,生猪市场价格是30元/斤,试估计该企业本养殖周期的销售收入是多少万元;
(3)若从本养殖周期的生猪中,任意选两头生猪,其重量达到270斤及以上的生猪数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com