
���� д��ԭ�����������⣬���жϢ٣�������Բ�Ķ��壬���жϢڣ�����ƽ������ͶӰ�Ķ��壬���жϢۣ����ݵȱ����еĶ��壬���жϢܣ�
��� �⣺�����⡰��x��1����x2-3x+2��0������������ǡ���x2-3x+2=0����x=1�����ʴ���
����֪��ԲA����x+1��2+y2=1��ԲB����x-1��2+y2=25����ԲM��ԲA���С���ԲB���У�
��Բ�ĵ���-1��0���ͣ�1��0������ľ����Ϊ��ֵ6��
��Բ��Բ��M�Ĺ켣����Բ������ȷ��
��������$\overrightarrow b=��{3��m}��$��$\overrightarrow a=��{1��\sqrt{3}}��$�����ϵ�ͶӰΪ3��
��$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|}$=$\frac{3+\sqrt{3}m}{2}$=3�����$m=\sqrt{3}$������ȷ��
��������{an}�У�a1=1��Sn����ǰn��ͣ�������${S_{n+1}}=\frac{1}{2}{S_n}+2$��
��n��2ʱ��${S}_{n}=\frac{1}{2}{S}_{n-1}+2$��
��ʽ����ã�an+1=$\frac{1}{2}$an��
��{an}�ǹ���Ϊ$\frac{1}{2}$�ĵȱ����У�����ȷ��
�ʴ�Ϊ���ڢۢܣ�
���� ���������������ж���Ӧ��Ϊ���壬�������������⣬��Բ�Ķ��壬������ͶӰ���ȱ����еĶ��壬�Ѷ��е���


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8}{3}\sqrt{7}$ | B�� | $\frac{16}{3}$ | C�� | $\frac{8}{3}$ | D�� | $\frac{16}{3}\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
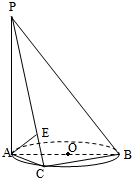 ��ͼ��ʾ����֪PA��ֱ��ԲO����ƽ�棬AB��ԲO��ֱ������ԲO��Բ��������A��B������һ�㣬��PA=AC����E���߶�PC���е㣮��֤��AE��ƽ��PBC��
��ͼ��ʾ����֪PA��ֱ��ԲO����ƽ�棬AB��ԲO��ֱ������ԲO��Բ��������A��B������һ�㣬��PA=AC����E���߶�PC���е㣮��֤��AE��ƽ��PBC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ֳ���������һ�ֲַ���� | |
| B�� | ���ֳ���������һ��ϵͳ���� | |
| C�� | �����������ɼ��ķ������������Ů���ɼ��ķ��� | |
| D�� | �ð༶�����ɼ���ƽ����С�ڸð�Ů���ɼ���ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD��ƽ���ı��Σ�AB��AC����AB=1��BC=2��PA�͵���ABCD��PA=$\sqrt{2}$����EΪ��BC������B��C�ĵ㣬��PE��ED��
��ͼ��������P-ABCD�У�����ABCD��ƽ���ı��Σ�AB��AC����AB=1��BC=2��PA�͵���ABCD��PA=$\sqrt{2}$����EΪ��BC������B��C�ĵ㣬��PE��ED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij����Ϊ���ƶ���ʱ�����Ҫȷ���ӹ���������ѵ�ʱ�䣬Ϊ�������Ĵ����飬�õ���
ij����Ϊ���ƶ���ʱ�����Ҫȷ���ӹ���������ѵ�ʱ�䣬Ϊ�������Ĵ����飬�õ���| ����ĸ���x������ | 2 | 3 | 4 | 5 |
| �ӹ���ʱ��y��Сʱ�� | 2.5 | 3 | 4 | 4.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2$\sqrt{3}$ | D�� | $\frac{3\sqrt{2}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com