
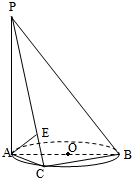
 如图所示,已知PA垂直于圆O所在平面,AB是圆O的直径,是圆O的圆周上异于A、B的任意一点,且PA=AC,点E是线段PC的中点.求证:AE⊥平面PBC.
如图所示,已知PA垂直于圆O所在平面,AB是圆O的直径,是圆O的圆周上异于A、B的任意一点,且PA=AC,点E是线段PC的中点.求证:AE⊥平面PBC. 分析 根据底面是圆,得到BC⊥AC,再根据PA⊥平面ABC得到PA⊥BC,即可证明BC⊥平面PAC,从而可证BC⊥AE,由PA=AC,点E为PC的中点,可证PC⊥AE,即可得证AE⊥平面PBC.
解答 证明:∵PA⊥⊙O所在的平面,BC?⊙O所在的平面,
∴PA⊥BC,
又∵AB是⊙O的直径,C是⊙O上一点,
∴AC⊥BC,
∵PA∩AC=A,
∴BC⊥平面PAC,
又∵AE在平面PAC内,
∴BC⊥AE.
∵PA=AC,点E为PC的中点
∴PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
点评 本题综合考查了线面垂直的判定与性质定理等基础知识与基本技能方法,考查了空间想象能力、推理能力和计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [$\frac{2}{3}$,+∞) | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com