
| A. | [$\frac{2}{3}$,1] | B. | [$\frac{2}{3}$,+∞) | C. | [1,+∞) | D. | [0,1] |
分析 由已知得f(a)≥1,当a≥1时,f(a)=2a≥1,当a<1时,f(a)=3a-1≥1,由此能求出a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≥1}\\{3x-1,x<1}\end{array}\right.$,f(f(a))=2f(a),
∴f(a)≥1,
当a≥1时,f(a)=2a≥1,解得a≥0,∴a≥1;
当a<1时,f(a)=3a-1≥1,解得a$≥\frac{2}{3}$,∴$\frac{2}{3}≤a<1$.
∴a的取值范围是[$\frac{2}{3}$,+∞).
故选:B.
点评 本题考查函数值的求法及应用,是基础题,解题时要认真审题,注意函数性质的合理运用.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2<x<3} | B. | {x|2≤x<3} | C. | {x|0≤x<3} | D. | {x|1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}\sqrt{7}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
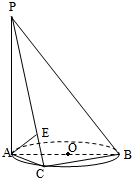 如图所示,已知PA垂直于圆O所在平面,AB是圆O的直径,是圆O的圆周上异于A、B的任意一点,且PA=AC,点E是线段PC的中点.求证:AE⊥平面PBC.
如图所示,已知PA垂直于圆O所在平面,AB是圆O的直径,是圆O的圆周上异于A、B的任意一点,且PA=AC,点E是线段PC的中点.求证:AE⊥平面PBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
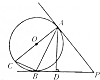 如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.
如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com