
分析 (1)依题意,得$\left\{{\begin{array}{l}{x'=\sqrt{3}x}\\{y'=2y}\end{array}}\right.$,则$\left\{{\begin{array}{l}{x=\frac{1}{{\sqrt{3}}}x'}\\{y=\frac{1}{2}y'}\end{array}}\right.$,代入x2+y2=1中,可得曲线C的方程为$\frac{x^2}{3}+\frac{y^2}{4}=1$,即可求曲线C的参数方程;
(2)求出直线PQ的直角坐标方程,与椭圆方程联立,可得AB的中点的坐标,求出线段AB的垂直平分线的方程,化为极坐标方程即可.
解答 解:(1)设(x',y')为曲线C上的点,圆上的点的坐标为(x,y),
依题意,得$\left\{{\begin{array}{l}{x'=\sqrt{3}x}\\{y'=2y}\end{array}}\right.$,则$\left\{{\begin{array}{l}{x=\frac{1}{{\sqrt{3}}}x'}\\{y=\frac{1}{2}y'}\end{array}}\right.$,代入x2+y2=1中,得$\frac{{{{x'}^2}}}{3}+\frac{{{{y'}^2}}}{4}=1$.
∴曲线C的方程为$\frac{x^2}{3}+\frac{y^2}{4}=1$,参数方程为$\left\{{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=2sinα}\end{array}}\right.(α$为参数)…(6分)
(2)∵点P$(2,\frac{2π}{3})$的直角坐标为$(-1,\sqrt{3})$,直线$θ=\frac{5π}{6}$的直角坐标方程为$y=-\frac{{\sqrt{3}}}{3}x$.
∴直线PQ的斜率为$\sqrt{3}$,直角坐标方程为$y-\sqrt{3}=\sqrt{3}(x+1)$,即$y=\sqrt{3}(x+2)$.
设A(x1,y1),B(x2,y2),联立$\left\{{\begin{array}{l}{y=\sqrt{3}(x+2)}\\{\frac{x^2}{3}+\frac{y^2}{4}=1}\end{array}}\right.$得13x2+36x+24=0.
∴${x_1}+{x_2}=-\frac{36}{13}$,∴AB的中点的坐标为$(-\frac{18}{13},\frac{{8\sqrt{3}}}{13})$.
∴线段AB的垂直平分线的方程为$y-\frac{{8\sqrt{3}}}{13}=-\frac{{\sqrt{3}}}{3}(x+\frac{18}{13})$,即$x+\sqrt{3}y-\frac{6}{13}=0$,
化为极坐标方程是$ρcosθ+\sqrt{3}ρsinθ-\frac{6}{13}=0$…(12分)
点评 本题考查曲线的参数方程、极坐标方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
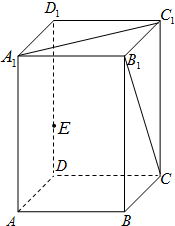 如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8,E为DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8,E为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解中学生的体能状况,某校抽取了n名高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中第二小组频数为7.
为了了解中学生的体能状况,某校抽取了n名高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中第二小组频数为7.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [$\frac{2}{3}$,+∞) | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π | |
| B. | 图象可由$y=\frac{1}{2}sinx$先把图象上各点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),再把所得图象向左平移$\frac{π}{8}$个单位长度而得到 | |
| C. | 图象关于直线x=$\frac{5π}{8}$对称 | |
| D. | 图象关于点($\frac{π}{8}$,0)对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com