Question

10．某车间为了制定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的

零件的个数x（个）	2	3	4	5
加工的时间y（小时）	2.5	3	4	4.5

数据如下：
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并在坐标系中画出回归直线；
（3）试预测加工10个零件需要多少小时？
（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）

Answer 1

分析 （1）根据表中所给的数据，可得散点图；
（2）求出出横标和纵标的平均数，得到样本中心点，求出对应的横标和纵标的积的和，求出横标的平方和，做出系数和a的值，写出线性回归方程．
（3）将x=10代入回归直线方程，可得结论．

解答 解：（1）作出散点图如下：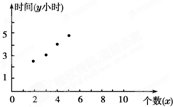
…（3分）
（2）$\overline{x}$=3.5，$\overline{y}$=3.5，…（5分）∧
$\sum_{i=1}^{4}$${{x}_{i}}^{2}$=54，$\sum_{i=1}^{4}$x_iy_i=52.5
∴$\stackrel{∧}{b}$=$\frac{52.5-4×3.5×3.5}{54-4×3．{5}^{2}}$=0.7
$\stackrel{∧}{a}$=3.5-0.7×3.5=1.05，
∴所求线性回归方程为：$\stackrel{∧}{y}$=0.7x+1.05…（10分）
（3）当x=10代入回归直线方程，得$\stackrel{∧}{y}$=0.7×10+1.05=8.05（小时）．
所以加工10个零件大约需要8.05个小时…（12分）

点评 本题考查线性回归方程的求法和应用，考查学生的计算能力，属于中档题．