
 如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为异面.(从相交、平行、异面、重合中选填)
如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为异面.(从相交、平行、异面、重合中选填)  小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}\sqrt{7}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,且AB=1,BC=2,PA⊥底面ABCD,PA=$\sqrt{2}$,又E为边BC上异于B,C的点,且PE⊥ED.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB⊥AC,且AB=1,BC=2,PA⊥底面ABCD,PA=$\sqrt{2}$,又E为边BC上异于B,C的点,且PE⊥ED.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某车间为了制定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的
某车间为了制定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
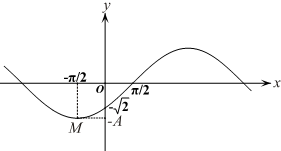 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点坐标为($\frac{π}{2}$,0),与y轴的交点坐标为(0,-$\sqrt{2}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点坐标为($\frac{π}{2}$,0),与y轴的交点坐标为(0,-$\sqrt{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
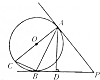 如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.
如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com