
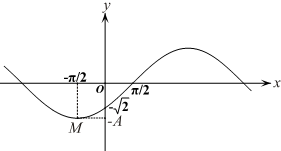
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点坐标为($\frac{π}{2}$,0),与y轴的交点坐标为(0,-$\sqrt{2}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点坐标为($\frac{π}{2}$,0),与y轴的交点坐标为(0,-$\sqrt{2}$).分析 (1)利用y=Asin(ωx+φ)的部分图象可求得其周期T=4π,从而可求得ω;由其图象与x轴的一个交点坐标为($\frac{π}{2}$,0)及|φ|<$\frac{π}{2}$可求得φ,当x=0时,y=Asin(-$\frac{π}{4}$)=-$\sqrt{2}$,可求得A;
(2)求出函数f(x)在x∈[0,2π]的取值情况,利用数形结合即可得到结论.
解答 解:(1)由图可知,函数的周期T=4×[$\frac{π}{2}$-(-$\frac{π}{2}$)]=4π,
∴$\frac{2π}{ω}$=4π,ω=$\frac{1}{2}$;
∵图象与x轴的一个交点坐标为($\frac{π}{2}$,0),
∴Asin($\frac{1}{2}$×$\frac{π}{2}$+φ)=0,
∴sin($\frac{π}{4}$+φ)=0,
∴$\frac{π}{4}$+φ=kπ,故φ=kπ-$\frac{π}{4}$(k∈Z).
由|φ|<$\frac{π}{2}$得,-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴φ=-$\frac{π}{4}$,
∴y=Asin($\frac{1}{2}$x-$\frac{π}{4}$).
当x=0时,y=Asin(-$\frac{π}{4}$)=-$\sqrt{2}$,
∴A=2.
综上可知,A=2,ω=$\frac{1}{2}$,φ=-$\frac{π}{4}$.
(2)由(1)可得:f(x)=2sin($\frac{1}{2}$x-$\frac{π}{4}$).
当x∈[0,2π]时,$\frac{1}{2}$x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],可得:f(x)=2sin($\frac{1}{2}$x-$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1].
由f(x)-m=0得f(x)=m,要使方程f(x)-m=0在x∈[0,2π]上有两个不同的解,
则f(x)=m在x∈[0,2π]上有两个不同的解,即函数f(x)和y=m在x∈[0,2π]上有两个不同的交点,
即$\frac{\sqrt{2}}{2}$≤m<1.
点评 本题考查y=Asin(ωx+φ)的部分图象确定函数解析式,求得A、ω、φ的值是关键,考查三角函数的图象和性质,考查了数形结合思想的应用,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | y=cos2x,x∈R | B. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R | C. | y=$sin|\frac{x}{2}|$,x?R | D. | y=x3+x,x?R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
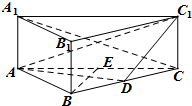 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
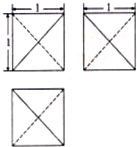
 如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为异面.(从相交、平行、异面、重合中选填)
如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为异面.(从相交、平行、异面、重合中选填)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+b2<c2 | B. | $\overrightarrow{AB}$•$\overrightarrow{AC}$<0 | C. | tanAtanB>1 | D. | $\overrightarrow{BC}$•$\overrightarrow{AB}$>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com