
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
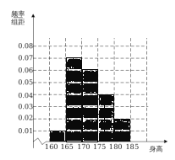
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
【答案】(1)直方图见解析;(2)![]() .
.
【解析】
(1)由题意知,0.050![]() ,从而n=100,由此求出第2组的频数和第3组的频率,并完成频率分布直方图.(2)利用分层抽样, 35名学生中抽取7名学生,设第1组的1位学生为
,从而n=100,由此求出第2组的频数和第3组的频率,并完成频率分布直方图.(2)利用分层抽样, 35名学生中抽取7名学生,设第1组的1位学生为![]() ,第4组的4位同学为
,第4组的4位同学为![]() ,第5组的2位同学为
,第5组的2位同学为![]() ,利用列举法能求出第4组中至少有一名学生被抽中的概率.
,利用列举法能求出第4组中至少有一名学生被抽中的概率.
(1)由频率分布表可得
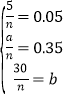 ,所以,
,所以,![]() ;
;
(2)因为第1,4,5组共有35名学生,利用分层抽样,在35名学生中抽取7名学生,每组分别为:第1组![]() ;第4组
;第4组![]() ;第5组
;第5组![]() .
.
设第1组的1位学生为![]() ,第4组的4位同学为
,第4组的4位同学为![]() ,第5组的2位同学为
,第5组的2位同学为![]() .
.
则从7位学生中抽两位学生的基本事件分别为:![]()
![]()
![]() 一共21种.
一共21种.
记“第4组中至少有一名学生被抽中”为事件![]() ,即
,即![]() 包含的基本事件分别为:
包含的基本事件分别为:![]() 一共3种,于是
一共3种,于是![]()
所以,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: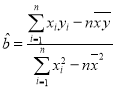 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
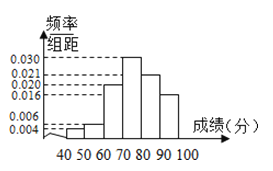
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若![]() ,则
,则![]() ; ②若
; ②若![]() 则
则![]() ;③若
;③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP. 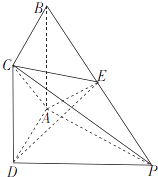
(1)证明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了![]() 户居民六月份的用电量(单位:
户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:
![]() .
.
对应的家庭收入数据如下:
![]()
![]() .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施![]() 阶阶梯电价,使
阶阶梯电价,使![]() 的用户在第一档,电价为
的用户在第一档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第二档,电价为
的用户在第二档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第三档,电价为
的用户在第三档,电价为![]() 元/
元/![]() ,试求出居民用电费用
,试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
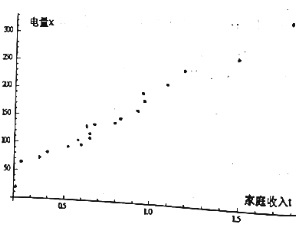
(Ⅱ)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).
(Ⅲ)小明家的月收入![]() 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() ,
,![]() ,…,
,…,![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为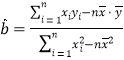 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
③若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 的最小值为
的最小值为![]()
正确的有__________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com