
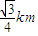 ,到点O的距离PO为
,到点O的距离PO为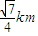 ,问下水管道AB能否经过污水总管的接口点P?若能,求出a的值,若不能,请说明理由.
,问下水管道AB能否经过污水总管的接口点P?若能,求出a的值,若不能,请说明理由.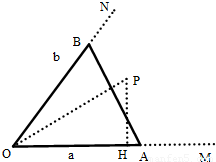
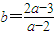 .
. .
.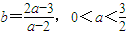 .
.
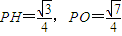 ,∴点P(
,∴点P(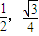 ).
).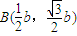 ,即B
,即B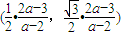 ,
,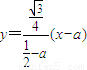 ,即
,即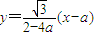 .
.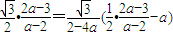 .
. .
.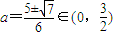 .
.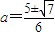 (km).
(km).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:
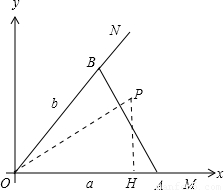
 (2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).
(2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)若道路的总长度不超过5.5 km,试求中心道长的取值范围.
(2)问中心道长为何值时,道路网的总长度最短?
查看答案和解析>>
科目:高中数学 来源:2012届江苏省高二下学期期末考试数学(理)试卷 题型:解答题
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com