
【题目】已知函数 ![]() .
.
(1)求函数y=f(x)的周期,并写出其单调递减区间;
(2)当 ![]() 时,求f(x)的最大值与最小值.
时,求f(x)的最大值与最小值.
【答案】
(1)解:函数 ![]() .
.
化简可得: ![]()
= ![]()
= ![]()
= ![]() ,
,
即 ![]()
函数的周期T= ![]() .
.
由2kπ+ ![]()
得k ![]()
∴f(x)的单调递减区间为 ![]() .
.
(2)解:当x ![]() 时,
时,
2x+ ![]() ,
,
∴ ![]() ≤sin(2x+
≤sin(2x+ ![]() )≤1.
)≤1.
故f(x)取得最大值 ![]() ;f(x)取得最小值
;f(x)取得最小值 ![]() .
.
【解析】(1)根据两角和的正弦公式和二倍角的余弦公式将f(x)进行化简可得f ( x ) = ![]() s i n ( 2 x +
s i n ( 2 x + ![]() ) + 1,根据周期公式和正弦函数的单调区间即可得出,(2)根据正弦函数的性质即可在给定区间得出f(x)的最大值和最小值.
) + 1,根据周期公式和正弦函数的单调区间即可得出,(2)根据正弦函数的性质即可在给定区间得出f(x)的最大值和最小值.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,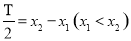 才能得出正确答案.
才能得出正确答案.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)﹣f(a)=f′(x0)(b﹣a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3﹣3x在区间[﹣2,2]上的“中值点”为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.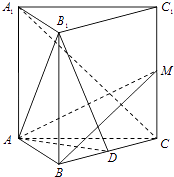
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),满足f(x﹣2)=﹣f(x),且当x∈[0,1]时,f(x)=x2+x+sinx,若方程f(x)=m(m>0)在区间[﹣4,4]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4的值为( )
A.2
B.﹣2
C.4
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣2
(Ⅰ)用定义法证明:函数f(x)在区间(﹣∞,1]上是减函数;
(Ⅱ)若函数g(x)=f(x)﹣mx是偶函数,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C:(x﹣5)2+(y+1)2=m(m>0)上有且只有一点到直线4x+3y﹣2=0的距离为1,则实数m的值为( )
A.4
B.16
C.4或16
D.2或4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com