
【题目】已知定义在R上的奇函数f(x),满足f(x﹣2)=﹣f(x),且当x∈[0,1]时,f(x)=x2+x+sinx,若方程f(x)=m(m>0)在区间[﹣4,4]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4的值为( )
A.2
B.﹣2
C.4
D.﹣4
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(
的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(![]() ) ,其中 m 为常数,且
) ,其中 m 为常数,且 ![]() .
.
①求证: ![]() 是等比数列;
是等比数列;
②若数列 ![]() 的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,
的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,![]() ,求证:
,求证: ![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1),n∈N* .
(1)求数列{an}的通项公式;
(2)若数列{bn}满足: ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )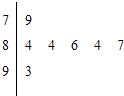
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①mn=nm类比得到ab=ba;
②(m+n)t=mt+nt类比得到(a+b)c=ac+bc;
③(mn)t=m(nt) 类比得到(ab)c=a(bc);
④t≠0,mt=rtm=r类比得到p≠0,ap=bpa=b;
⑤|mn|=|m||n|类比得到|ab|=|a||b|;
⑥ ![]() =
= ![]() 类比得到
类比得到 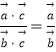 .
.
以上式子中,类比得到的结论正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 
(Ⅰ)求出f(5);
(Ⅱ)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com