
【题目】设数列![]() 的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(
的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(![]() ) ,其中 m 为常数,且
) ,其中 m 为常数,且 ![]() .
.
①求证: ![]() 是等比数列;
是等比数列;
②若数列 ![]() 的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,
的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,![]() ,求证:
,求证: ![]() 为等差数列.
为等差数列.
【答案】【解答】解:①由 (3-m)Sn+2man=m+3 ,得(3-m)Sn+1+2man+1=m+3 ,
两式相减,得(3+m)an+1=2man (![]() ) ,
) ,
∴![]() .
.
又m为常数,且 ![]() ,∴
,∴ ![]() 是等比数列.
是等比数列.
②∵ (3-m)Sn+2man=m+3 ,
∴(3-m)a1+2ma1=m+3 .
∴ a1=1,b1=a=1, .
由①可得,![]() .
.
∴ 当 ![]() ,且
,且 ![]() 时,
时, ![]() .∴
.∴![]() .
.
∴![]() .
.
∴数列![]() 是首项为1,公差为
是首项为1,公差为 ![]() 的等差数列.
的等差数列.
【解析】本题主要考查了分析法与综合法,解决问题的关键是需要利用等比数列、等差数列的定义使用综合法加以证明,解题的关键是恰当地处理递推关系.
综合法证明数列问题时的证明依据主要来源于以下数列的相关知识:(1)数列的概念,特别是等差数列、等比数列的定义;(2)等差数列与等比数列的基本性质以及数列前 n 项和的性质;(3)数列的通项公式 an 与数列的前 n 项和 Sn 之间的关系 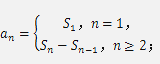 (4)递推公式与通项公式的关系.
(4)递推公式与通项公式的关系.


科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的左、右焦点分别为F1 , F2 , 弦AB过F1 , 若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1 , y1),(x2 , y2),则|y1﹣y2|的值为 .
的左、右焦点分别为F1 , F2 , 弦AB过F1 , 若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1 , y1),(x2 , y2),则|y1﹣y2|的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3x2﹣2x,数列{an}的前n项和为Sn , 点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对应的边分别为a,b,c,若c(acosB﹣ ![]() b)=a2﹣b2 .
b)=a2﹣b2 .
(1)求角A;
(2)若a= ![]() ,求c﹣b的取值范围.
,求c﹣b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)﹣f(a)=f′(x0)(b﹣a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3﹣3x在区间[﹣2,2]上的“中值点”为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),满足f(x﹣2)=﹣f(x),且当x∈[0,1]时,f(x)=x2+x+sinx,若方程f(x)=m(m>0)在区间[﹣4,4]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4的值为( )
A.2
B.﹣2
C.4
D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com