
【题目】设a,b,c为正实数,且满足abc=1,试证明:![]() +
+![]() +
+![]() ≥
≥![]() .
.
【答案】解:由abc=1,得 ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,则原不等式等价于
,则原不等式等价于![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
证法一:运用柯西不等式,有
(ab+bc+ca)2=( ![]() +
+![]() +
+![]() )2
)2
≤( ![]() +
+ ![]() +
+ ![]() )(ca+cb+ab+ac+ab+bc),
)(ca+cb+ab+ac+ab+bc),
于是, ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() (ab+bc+ca)≥
(ab+bc+ca)≥ ![]() ·3
·3 ![]() =
=![]() .
.
证法二:由基本不等式得![]() +
+ ![]() ≥2
≥2 ![]() =bc.
=bc.![]() +
+![]() ≥ac,
≥ac, ![]() +
+ ![]() ≥ab,
≥ab,
相加得![]() +
+ ![]() +
+ ![]() ≥
≥![]() (ab+ca+bc)≥
(ab+ca+bc)≥ ![]() ·3
·3 ![]() =
= ![]() .
.
证法三:设s=![]() ·bc+
·bc+![]() ·ac+
·ac+![]() ·ab.
·ab.
设a≤b≤c,则ab≤ac≤bc,ab+ac≤ab+bc≤ac+bc.
于是 ![]() ≥
≥ ![]() ≥
≥ ![]() ,由此推知s为顺序和,由排序不等式得
,由此推知s为顺序和,由排序不等式得
s≥ ![]() ·ac+
·ac+ ![]() ·ab+
·ab+ ![]() ·bc=
·bc=![]() +
+![]() +
+![]() ,
,
s≥ ![]() ·ab+
·ab+ ![]() ·bc+
·bc+ ![]() ·ac=
·ac= ![]() +
+ ![]() +
+![]() ,
,
相加得
2s≥ ![]() +
+ ![]() +
+ ![]() ≥3
≥3 ![]() =3,所以s≥
=3,所以s≥ ![]() .
.
【解析】本题主要考查了排序不等式,解决问题的关键是设a≤b≤c,则ab≤ac≤bc,ab+ac≤ab+bc≤ac+bc.于是 ![]() ≥
≥ ![]() ≥
≥ ![]() ,由此推知s为顺序和,由排序不等式分析分组相加即可证明
,由此推知s为顺序和,由排序不等式分析分组相加即可证明
【考点精析】根据题目的已知条件,利用排序不等式的相关知识可以得到问题的答案,需要掌握排序不等式(排序原理):设![]() 为两组实数.
为两组实数.![]() 是
是![]() 的任一排列,则
的任一排列,则![]()
![]() (反序和
(反序和![]() 乱序和
乱序和![]() 顺序和)当且仅当
顺序和)当且仅当![]() 或
或![]() 时,反序和等于顺序和.
时,反序和等于顺序和.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】对任意实数x,[x]表示不超过x的最大整数,如[3.6]=3,[﹣3.6]=﹣4,关于函数f(x)=[ ![]() ﹣[
﹣[ ![]() ]],有下列命题: ①f(x)是周期函数;
]],有下列命题: ①f(x)是周期函数;
②f(x)是偶函数;
③函数f(x)的值域为{0,1};
④函数g(x)=f(x)﹣cosπx在区间(0,π)内有两个不同的零点,
其中正确的命题为(把正确答案的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个科研小组有4位男组员和2位女组员,其中一位男组员和一位女组员不会英语,其他组员都会英语,现在要用抽签的方法从中选出两名组员组成一个科研攻关小组.
(Ⅰ)求组成攻关小组的成员是同性的概率;
(Ⅱ)求组成攻关小组的成员中有会英语的概率;
(Ⅲ)求组成攻关小组的成员中有会英语并且是异性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则下列说法正确的是( )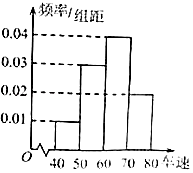
A.平均数为62.5
B.中位数为62.5
C.众数为60和70
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(
的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(![]() ) ,其中 m 为常数,且
) ,其中 m 为常数,且 ![]() .
.
①求证: ![]() 是等比数列;
是等比数列;
②若数列 ![]() 的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,
的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,![]() ,求证:
,求证: ![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1),n∈N* .
(1)求数列{an}的通项公式;
(2)若数列{bn}满足: ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com