
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
【答案】
(1)解:某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,
每个旅游团可任选其中一条旅游线路,基本事件总数n=42=16,
甲、乙两个旅游团所选旅游线路不同包含的基本事件个数m= ![]() =4×3=12,
=4×3=12,
∴甲、乙两个旅游团所选旅游线路不同的概率:
p= ![]()
(2)解:设甲、乙两个旅游团到达著名景点的时刻分别为x,y,
依题意得  ,即
,即 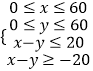 ,
,
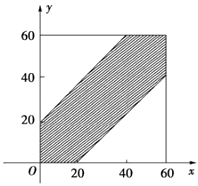
作出不等式表示的区域,如图:
记“两个旅游团在著名景点相遇”为事件B,
P(B)= ![]() =
= ![]() .
.
∴两个旅游团在该著名景点相遇的概率为 ![]() .
.
【解析】(1)每个旅游团可任选其中一条旅游线路,基本事件总数n=42=16,甲、乙两个旅游团所选旅游线路不同包含的基本事件个数m= ![]() =4×3=12,由此能求出甲、乙两个旅游团所选旅游线路不同的概率.(2)设甲、乙两个旅游团到达著名景点的时刻分别为x,y,依题意得
=4×3=12,由此能求出甲、乙两个旅游团所选旅游线路不同的概率.(2)设甲、乙两个旅游团到达著名景点的时刻分别为x,y,依题意得  ,由此利用几何概型能求出两个旅游团在该著名景点相遇的概率.
,由此利用几何概型能求出两个旅游团在该著名景点相遇的概率.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以 ![]() 为概率的事件是( )
为概率的事件是( )
A.都不是一等品
B.恰有一件一等品
C.至少有一件一等品
D.至多一件一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1),n∈N* .
(1)求数列{an}的通项公式;
(2)若数列{bn}满足: ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com