
 ,对于图二,
,对于图二,

 ,CE=
,CE= ,
,
 ,∴AC=2
,∴AC=2
 ,
, ,∴
,∴
 ,又BC∩CD=C,∴AC⊥平面BCD;
,又BC∩CD=C,∴AC⊥平面BCD; 平面ABD,
平面ABD, ;
; ,∴
,∴
 ,于是AC与平面ABD所成角
,于是AC与平面ABD所成角 的正弦为sin
的正弦为sin =
= ;
; =(x,y,z),则
=(x,y,z),则 ·
· =0,
=0, ·
· =0
=0 2x-2z=0,y-2z=0
2x-2z=0,y-2z=0 =(1,1,1),于是AC与平面ABD所成角
=(1,1,1),于是AC与平面ABD所成角 的正弦即:
的正弦即:


科目:高中数学 来源: 题型:
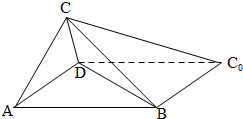 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
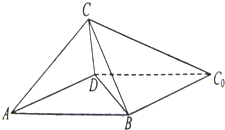 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间向量及其运算、角的概念及其求法和空间距离专项训练(河北) 题型:解答题
如右图所示,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=.沿它的对角线BD把△BDC0折起,使点C0到达平面ABC0D外点C的位置.
(1)证明:平面ABC0D⊥平面CBC0;
(2)如果△ABC为等腰三角形,求二面角A-BD-C的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若F2(2,0)关于直线y=![]() x+
x+![]() 的对称点在椭圆E上,求该椭圆E的方程;
的对称点在椭圆E上,求该椭圆E的方程;
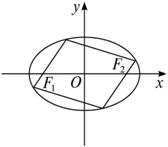
(2)若椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),求这个平行四边形面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com