
| 成绩 | 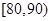 | 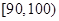 | 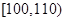 | 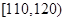 | 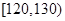 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 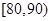 | 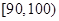 | 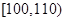 | 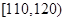 | 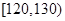 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
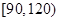 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;| | 成绩小于100分 | 成绩不小于100分 | 合计 |
| 甲班 | 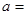 | 26 | 50 |
| 乙班 | 12 | 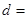 | 50 |
| 合计 | 36 | 64 | 100 |
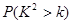 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
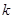 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:单选题
 ,净重大于等于15克且小于17克的产品数为
,净重大于等于15克且小于17克的产品数为 ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出 和
和 分别为( )
分别为( )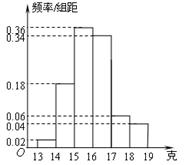
A. | B. |
C.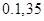 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
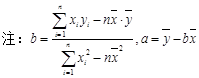
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
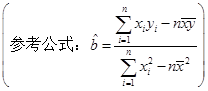
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com