练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．下列说法中，正确的是（　　）
    A．钝角必是第二象限角，第二象限角必是钝角
    B．第三象限的角必大于第二象限的角
    C．小于90°的角是锐角
    D．-95°20′，984°40′，264°40′是终边相同的角

    分析 根据角的大小关系以及象限角的定义分别进行判断即可．

    解答 解：A．钝角必是第二象限角，正确，但二象限角必是钝角错误，比如α=480°是二象限角但不是钝角，故A错误，
    B．第三象限的角必大于第二象限的角，比如α=-100°是第三象限角，β=120°是第二象限角，则＜β，故B错误，
    C．小于90°的角是锐角错误，比如α=0°＜90°，但α不是锐角，故C错误，
    D．-95°20′=-360°+264°40′，984°40′=2×360°+264°40′，则三个角的终边相同，是终边相同的角，故D正确
    故选：D

    点评 本题主要考查命题的真假判断，涉及角的大小比较以及象限角的定义，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|，则$\overrightarrow{a}$与$\overrightarrow{b}$-$\overrightarrow{a}$夹角为（　　）
    A．$\frac{5}{6}π$B．$\frac{2}{3}π$C．$\frac{1}{6}π$D．$\frac{1}{3}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

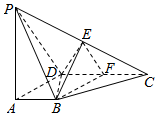    5．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠DAB为直角，AB∥CD，AD=CD=2AB=2，E，F分别为PC，CD的中点．
    （Ⅰ）证明：AB⊥平面BEF：
    （Ⅱ）设PA=h，若二面角E-BD-C大于45°，求h的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，AP=1，AD=2，E为线段PD上一点，记$\frac{PE}{PD}$=λ． 当λ=$\frac{1}{2}$时，二面角D-AE-C的平面角的余弦值为$\frac{2}{3}$．
    （1）求AB的长；
    （2）当$λ=\frac{2}{3}$时，求异面直线BP与直线CE所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知数列{an}中，a1=1，an+1=$\frac{\sqrt{2}{a}_{n}}{\sqrt{{{a}_{n}}^{2}+2}}$（n∈N*）
    （1）证明{$\frac{1}{{{a}_{n}}^{2}}$}是等差数列，并求数列{an}的通项公式；
    （2）设bn=$\frac{1}{{{a}_{n}}^{2}}$，数列{bn}的前n项和为Sn，已知存在正整数m，使得$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$＜m对n∈N+恒成立，求m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．由曲线y=-x2+x+2与其在点A（2，0）和点B（-1，0）处的切线所围成图形的面积为$\frac{9}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知$f（x）=x+\frac{1}{x}$
    （1）求函数在$x=\frac{1}{2}$处的切线方程．
    （2）求函数在x=x0处的切线与直线y=x和y轴围成的三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直线l的参数方程为$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{6}}{3}t}\\{y=\frac{\sqrt{3}}{3}t}\end{array}\right.$（t为参数），在直角坐标系中，以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的方程为ρ=2$\sqrt{2}$cos（θ-$\frac{π}{4}$）-2sinθ．
    （1）求曲线C的直角坐标方程；
    （2）点P、Q分别为直线l与曲线C上的动点，求|PQ|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．（1）已知$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是夹角为60°的两个单位向量，$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$，求$\overrightarrow{a}$•$\overrightarrow{b}$；
    （2）已知$\overrightarrow a=（3，4），\overrightarrow b=（2，-1），求$$\overrightarrow{a}$•$\overrightarrow{b}$，$\overrightarrow a在\overrightarrow b方向上的投影$．

    查看答案和解析>>

    同步练习册答案