
分析 欲求切线的方程,只须求出其斜率的值即可,故先利用导数求出在切点处的导函数值,再结合A(2,0)和点B(-1,0)都在抛物线上,即可求出切线的方程,然后可得直线与抛物线的交点的坐标和两切线与x轴交点的坐标,最后根据定积分在求面积中的应用公式即可求得所围成的面积S即可.
解答 解:对y=-x2+x+2求导可得,y′=-2x+1
∴抛物线=-x2+x+2在点A(2,0)和点B(-1,0)处的两条切线的斜率分别为-3,3
从而可得曲线y=-x2+x+2在点A(2,0)和点B(-1,0)处的两条切线方程分别为
l1:3x+y-6=0,l2:3x-y+3=0
联立,求得交点C($\frac{1}{2}$,$\frac{9}{2}$).
所以S=S△ABC-${∫}_{-1}^{2}$(-x2+x+2)dx=$\frac{1}{2}×3×\frac{9}{2}$-(-$\frac{1}{3}$x3+$\frac{1}{2}$x2+2x)${|}_{-1}^{2}$=$\frac{27}{4}$-$\frac{9}{2}$=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程、定积分在求面积中的应用等基础知识,考查运算求解能力.属于中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
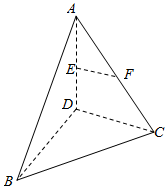 如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AD、AC的中点,BC⊥CD.
如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AD、AC的中点,BC⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角必是第二象限角,第二象限角必是钝角 | |
| B. | 第三象限的角必大于第二象限的角 | |
| C. | 小于90°的角是锐角 | |
| D. | -95°20′,984°40′,264°40′是终边相同的角 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com