Question

17．已知异面直线a、b成80°角，A为空间中一点，则过A与a、b都成40°角的平面共有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 过A作a，b的平行线a′，b′，则a′，b′所成夹角为80°或100°，设a′，b′确定的平面为α，符合条件的平面为β，α∩β=l，则l平分a′，b′的夹角，且α⊥β时，a′，b′与平面β所成的角最大．根据平面的对称性即可得出符合条件的平面β的个数．

解答 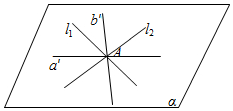解：过A作a′∥a，b′∥b，设直线a′、b′确定的平面为α，
∵异面直线a、b成80°角，∴直线a′、b′确所成锐角为80°．
设过A点的平面β与a′，b′所成的角相等，α∩β=l，则l平分a′，b′所成的锐角或钝角．
（1）若l平方a′，b′所成的锐角，则当α⊥β时，直线a′，b′与平面β所成的角最大，最大角为40°，
故此时符合条件的平面只有一个．
（2）若l平分a′，b′所成的钝角，则当α⊥β时，直线a′，b′与平面β所成的角最大，最大角为50°，
有对称性可知此时符合条件的平面有2个．
又a′∥a，b′∥b，∴a，b与平面β所成的角等于a′，b′与平面β所成的角．
所以过A与a、b都成40°角的平面共有3个．
故选：C．

点评 本题考查了看见线面位置关系的判断，结合图形寻找线面角的最大值是关键．