练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)具有如下两个性质：

    (1)对任意的x1，x2∈R(x1≠x2)有＞0；

    (2)图象关于点(1，0)成中心对称图形．写出f(x)的一个解析表达式________．(只要求写一个表达式即可)．

    答案：
    解析：

    y＝x－1(不唯一)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：022

    (2007北京丰台模拟)定义在实数R上的函数y=f(x)具有如下性质：

    ①对任意x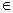R，都有；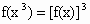

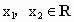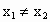    ②对任意且，都有．

    则f(－1)＋f(0)＋f(1)=________．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：022

    已知函数f(x)具有如下的性质：

    ①若f(x1)＝f(x2)，x1≠x2，则x1＋x2＝2．②若x1，x2∈(1，＋∞)，x1≠x2，则点(x1，f(x1))与点(x2，f(x2))的连线的斜率大于零．写出符合条件的一个函数：________．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：填空题

    已知函数f(x)具有如下两个性质：①对任意的x1，x2∈R(x1≠x2)都有；②图象关于点(1，0)成中心对称图形，写出函数f(x)的一个解析表达式为（    ）。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)具有如下两个性质：①对任意的x1，x2∈R(x1≠x2)都有>0；②图象关于点(1,0)成中心对称图形．写出函数f(x)的一个解析表达式为______________________________________．

    查看答案和解析>>

    同步练习册答案