
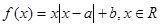 .
.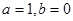 时,判断
时,判断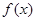 的奇偶性,并说明理由;
的奇偶性,并说明理由;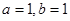 时,若
时,若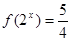 ,求
,求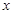 的值;
的值;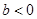 ,且对任何
,且对任何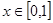 不等式
不等式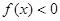 恒成立,求实数
恒成立,求实数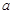 的取值范围.
的取值范围.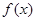 既不是奇函数,也不是偶函数;(2)所以
既不是奇函数,也不是偶函数;(2)所以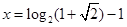 或
或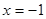 ;(3)当
;(3)当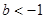 时,
时,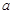 的取值范围是
的取值范围是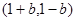 ,当
,当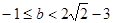 时,
时,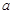 的取值范围是
的取值范围是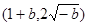 ;当
;当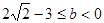 时,
时,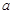 的取值范围是
的取值范围是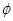 .
.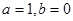 时,
时,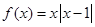 为确定的函数,要证明它具有奇偶性,必须按照定义证明,若要说明它没有奇偶性,可举一特例,说明某一对值
为确定的函数,要证明它具有奇偶性,必须按照定义证明,若要说明它没有奇偶性,可举一特例,说明某一对值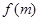 与
与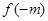 不相等(不是偶函数)也不相反(不是奇函数).(2)当
不相等(不是偶函数)也不相反(不是奇函数).(2)当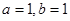 时,
时,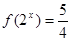 为
为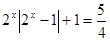 ,这是含有绝对值符号的方程,要解这个方程一般是分类讨论绝对值符号里的式子
,这是含有绝对值符号的方程,要解这个方程一般是分类讨论绝对值符号里的式子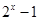 的正负,以根据绝对值定义去掉绝对值符号,变成通常的方程来解.(3)不等式
的正负,以根据绝对值定义去掉绝对值符号,变成通常的方程来解.(3)不等式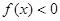 恒成立时要求参数
恒成立时要求参数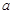 的取值范围,一般要把问题进行转化,例如分离参数法,或者转化为函数的最值问题.
的取值范围,一般要把问题进行转化,例如分离参数法,或者转化为函数的最值问题.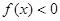 即为
即为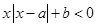 ,可以先把绝对值式子
,可以先把绝对值式子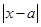 解出来,这时注意首先把
解出来,这时注意首先把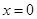 分出来,然后讨论
分出来,然后讨论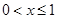 时,不等式化为
时,不等式化为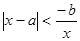 ,于是有
,于是有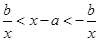 ,即
,即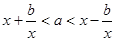 ,这个不等式恒成立,说明
,这个不等式恒成立,说明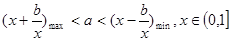 ,这时我们的问题就转化为求函数
,这时我们的问题就转化为求函数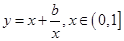 的最大值,求函数
的最大值,求函数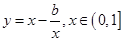 的最小值.
的最小值.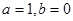 时,
时,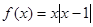 既不是奇函数也不是偶函数(2分)
既不是奇函数也不是偶函数(2分)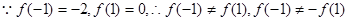
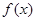 既不是奇函数,也不是偶函数 (4分)
既不是奇函数,也不是偶函数 (4分)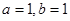 时,
时,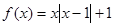 ,
,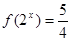 得
得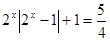 (1分)
(1分)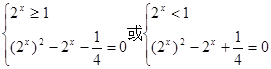 (3分)
(3分)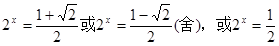 (5分)
(5分)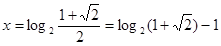 或
或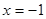 (6分)
(6分)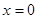 时,
时,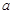 取任意实数,不等式
取任意实数,不等式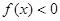 恒成立,
恒成立,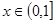 ,此时原不等式变为
,此时原不等式变为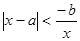 (1分)
(1分)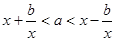
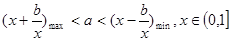
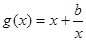 在
在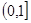 上单调递增,所以
上单调递增,所以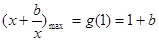 ;(2分)
;(2分)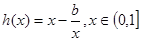
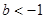 时,在
时,在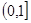 上
上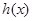 单调递减,
单调递减,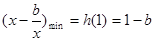 ,又
,又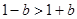 ,
,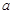 的取值范围是
的取值范围是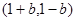 (3分)
(3分)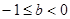 ,在
,在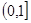 上,
上,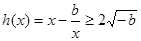 ,
,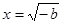 时,
时,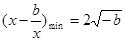 ,此时要使
,此时要使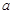 存在,
存在,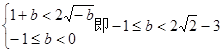 ,此时
,此时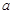 的取值范围是
的取值范围是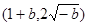 (4分)
(4分)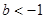 时,
时,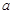 的取值范围是
的取值范围是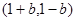
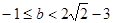 时,
时,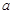 的取值范围是
的取值范围是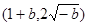 ;
;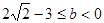 时,
时,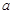 的取值范围是
的取值范围是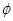 (6分)
(6分)

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:不详 题型:单选题
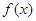 的图象形如字母M,奇函数
的图象形如字母M,奇函数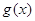 的图象形如字母N,若方程:
的图象形如字母N,若方程: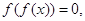
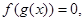
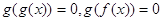 的实数根的个数分别为a、b、c、d,则
的实数根的个数分别为a、b、c、d,则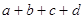 =( )
=( ) 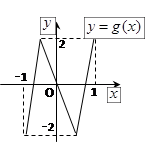
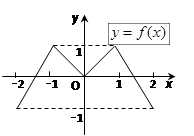
| A.27 | B.30 | C.33 | D.36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com