
【题目】将函数 ![]() 的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为 .
的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为 .
【答案】![]()
【解析】解:将函数 ![]() 的图象向左平移φ(φ>0)个单位后, 所得到的图象对应的函数解析式为y=2sin[3(x+φ)﹣
的图象向左平移φ(φ>0)个单位后, 所得到的图象对应的函数解析式为y=2sin[3(x+φ)﹣ ![]() ]=2sin(3x+3φ﹣
]=2sin(3x+3φ﹣ ![]() ),
),
再由y=sin(3x+3φ﹣ ![]() )为奇函数,
)为奇函数,
可得3φ﹣ ![]() =kπ,k∈z,
=kπ,k∈z,
可得φ= ![]() kπ+
kπ+ ![]() ,k∈z,
,k∈z,
由于φ>0,
则φ的最小值为 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上.
)=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)若圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x2﹣ax+1+a)在区间(﹣∞,2)上为减函数,则a的取值范围为( )
A.[4,+∞)
B.[4,5]
C.(4,5)
D.[4,5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高三年级学生寒假期间的学习情况,某学校抽取了甲、乙两班作为对象,调查这两个班的学生在寒假期间平均每天学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生平均每天学习时间在区间![]() 的有8人.
的有8人.
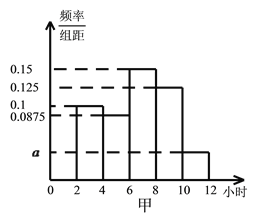

(I)求直方图中![]() 的值及甲班学生平均每天学习时间在区间
的值及甲班学生平均每天学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班平均每天学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+2sinxcosx+2cos2x.
(1)求f(x)递增区间;
(2)求f(x)的对称轴方程;
(3)求f(x)的最大值并写出取最大值时自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE. 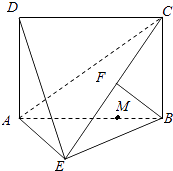
(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com