
【题目】已知函数f(x)=log2(x2﹣ax+1+a)在区间(﹣∞,2)上为减函数,则a的取值范围为( )
A.[4,+∞)
B.[4,5]
C.(4,5)
D.[4,5)
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x,则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn,若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是____.(只填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
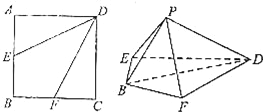
【题目】
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ ![]() (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈(﹣1,+∞)时,证明:f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组数开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是 . (下列摘取了随机数表第1行至第5行) 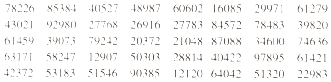
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com