
 ×4]-72=-2n2+40n-72
×4]-72=-2n2+40n-72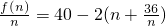
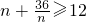
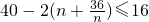

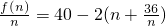 ,再利用基本不等式,即可求得年平均纯利润的最大值.
,再利用基本不等式,即可求得年平均纯利润的最大值.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
 ,道路C、E上下班时间往返出现拥堵的概率都是
,道路C、E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B.
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 对于具有线性相关关系的一组数据(见右表):用最小二乘法求得线性回归方程
对于具有线性相关关系的一组数据(见右表):用最小二乘法求得线性回归方程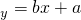 ,经过一点(样本中心点)是
,经过一点(样本中心点)是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com