
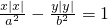 ,给出以下结论:
,给出以下结论: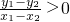
 -
- =1,图象是焦点在x轴上的双曲线位于第一象限内的部分,
=1,图象是焦点在x轴上的双曲线位于第一象限内的部分, +
+ =1,图象是椭圆在第四象限内的部分,
=1,图象是椭圆在第四象限内的部分, +
+ =-1,不表示任何图形,
=-1,不表示任何图形, -
- =1,图象是焦点在y轴上的双曲线位于第三象限内的部分.
=1,图象是焦点在y轴上的双曲线位于第三象限内的部分.

科目:高中数学 来源: 题型:
| d2 |
| d1 |
| ||
| 2 |
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
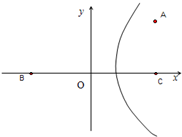 A村在C村正北
A村在C村正北| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
已知直线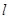 :
: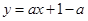
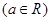 .若存在实数
.若存在实数 使得一条曲线与直线
使得一条曲线与直线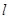 有两个不同的交点,且以这两个交点为端点的线段长度恰好等于
有两个不同的交点,且以这两个交点为端点的线段长度恰好等于 ,则称此曲线为直线
,则称此曲线为直线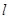 的“绝对曲线”.下面给出四条曲线方程:①
的“绝对曲线”.下面给出四条曲线方程:①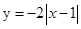 ;②
;②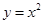 ;③
;③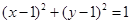 ;④
;④ ;则其中直线
;则其中直线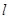 的“绝对曲线”有
( )
的“绝对曲线”有
( )
A.①④ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北荆州、黄冈、襄阳、十堰、宜昌、孝感、恩施七市高三4月联考理数学卷(解析版) 题型:选择题
已知直线l:y=ax+1-a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y="-2"
|x-1|;②y=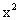 ;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
A.①④ B.②③ C.②④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com