
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
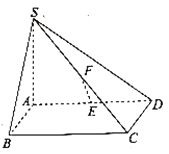
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由中位线定理可证,
,由中位线定理可证,![]() ,再由已知条件可得
,再由已知条件可得![]() ,可证四边形
,可证四边形![]() 为平行四边形,即可得证结论;
为平行四边形,即可得证结论;
(2)![]() 平面
平面![]() ,点
,点![]() 到平面
到平面![]() 的距离相等,转化为求
的距离相等,转化为求![]() 到平面
到平面![]() 的距离相等,连接
的距离相等,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可证
,可证![]() ,结合已知可得
,结合已知可得![]() 平面
平面![]() ,由直线与平面所成角的定义,得
,由直线与平面所成角的定义,得![]() ,根据直角三角形边角关系及中位线定理,求出
,根据直角三角形边角关系及中位线定理,求出![]() ,可得
,可得![]() ,由已知条件可得
,由已知条件可得![]() 平面
平面![]() ,进而有
,进而有![]() ,可证
,可证![]() 平面
平面![]() ,
,![]() 为所求距离;或求出三棱锥
为所求距离;或求出三棱锥![]() 的体积和
的体积和![]() 的面积,用等体积法,求点
的面积,用等体积法,求点![]() 到平面
到平面![]() 的距离
的距离
解:(1)证明:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() .又∵
.又∵![]() 为
为![]() 中点,底面
中点,底面![]() 是矩形,
是矩形,
∴![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.

(2)方法一:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 与平面
与平面![]() 所成角为
所成角为![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∵底面![]() 为矩形,∴
为矩形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,
,![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

方法二:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∵底面![]() 为矩形,∴
为矩形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则
由![]() 得
得![]() .
.
∴![]() ,∴
,∴![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.



科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为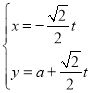 (t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设与圆O:![]() 相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的点(点
上的点(点![]() 与
与![]() 、
、![]() 不重合),则下列结论正确的个数为( )
不重合),则下列结论正确的个数为( )
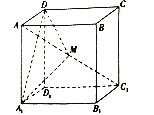
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③若![]() 的面积为
的面积为![]() ,则
,则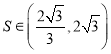 ;
;
④若![]() 、
、![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为A,且椭圆E经过
的左顶点为A,且椭圆E经过![]() 与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为
与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为![]() .
.
(I)求椭圆E的标准方程;
(Ⅱ)求证:直线l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线为
处的切线为![]() ,若函数
,若函数![]() 满足
满足![]() (其中
(其中![]() 为函数
为函数![]() 的定义域,当
的定义域,当![]() 时,
时,![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的“转折点”,已知函数
的“转折点”,已知函数![]() 在区间
在区间![]() 上存在一个“转折点”,则
上存在一个“转折点”,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得
天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界军人运动会,简称“军运会”,是国际军事体育理事会主办的全球军人最高规格的大型综合性运动会,每四年举办一届,会期7至10天,比赛设27个大项,参赛规模约100多个国家8000余人,规模仅次于奥运会,是和平时期各国军队展示实力形象、增进友好交流、扩大国际影响的重要平台,被誉为“军人奥运会”.根据各方达成的共识,军运会于2019年10月18日至27日在武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项、329个小项.其中,空军五项、军事五项、海军五项、定向越野和跳伞5个项目为军事特色项目,其他项目为奥运项目.现对某国在射击比赛预赛中的得分数据进行分析,得到如下的频率分布直方图:
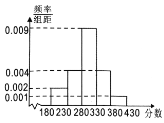
(1)估计某国射击比赛预赛成绩得分的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据大量的射击成绩测试数据,可以认为射击成绩![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50,用样本平均数
的近似值为50,用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,求射击成绩得分
的估计值,求射击成绩得分![]() 恰在350到400的概率;[参考数据:若随机变量
恰在350到400的概率;[参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则:
,则:![]() ,
,![]() ,
,![]() ;
;
(3)某汽车销售公司在军运会期间推广一款新能源汽车,现面向意向客户推出“玩游戏,送大奖”,活动,客户可根据抛掷骰子的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知骰子出现任意点数的概率都是![]() ,方格图上标有第0格,第1格,第2格,……第50格.遥控车开始在第0格,客户每抛掷一次骰子,遥控车向前移动一次,若抛掷出正面向上的点数是1,2,3,4,5点,遥控车向前移动一格(从
,方格图上标有第0格,第1格,第2格,……第50格.遥控车开始在第0格,客户每抛掷一次骰子,遥控车向前移动一次,若抛掷出正面向上的点数是1,2,3,4,5点,遥控车向前移动一格(从![]() 到
到![]() ),若抛掷出正面向上的点数是6点,遥控车向前移动两格(从
),若抛掷出正面向上的点数是6点,遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移动到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移动到第
),直到遥控车移动到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移动到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() ,以及根据
,以及根据![]() 的值解释这种游戏方案对意向客户是否具有吸引力.
的值解释这种游戏方案对意向客户是否具有吸引力.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com