
 ,证明:φ(x)∈A;
,证明:φ(x)∈A;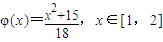 ,是否存在设x∈(1,2),使得x=φ(2x),如存在,求出所有的x,如不存在请说明理由!
,是否存在设x∈(1,2),使得x=φ(2x),如存在,求出所有的x,如不存在请说明理由!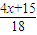 ,x∈[1,2],
,x∈[1,2],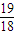 ≤φ(2x)≤
≤φ(2x)≤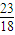 ∴φ(2x)∈(1,2);
∴φ(2x)∈(1,2);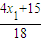 -
-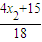 |=
|= ||x1-x2|
||x1-x2| ∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立
∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立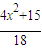 ,x∈(1,2),
,x∈(1,2),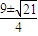
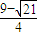 ∈(1,2),
∈(1,2),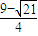 ∈(1,2),使得x=φ(2x).
∈(1,2),使得x=φ(2x).

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
| 2x+15 |
| 18 |
| x2+15 |
| 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 1+x |
| Lk-1 |
| 1-L |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
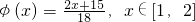 ,证明:φ(x)∈A;
,证明:φ(x)∈A;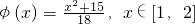 ,是否存在设x0∈(1,2),使得x0=φ(2x0),如存在,求出所有的x0,如不存在请说明理由!
,是否存在设x0∈(1,2),使得x0=φ(2x0),如存在,求出所有的x0,如不存在请说明理由!查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com