
分析 (1)(2)(3)(4)(5),首先求出原函数的值域,把原函数表达式看做方程,用y表示x,再把x与y互换,即可得出原函数的反函数及其定义域(即原函数的值域).
解答 解:(1)由y=x2-2x-3=(x-1)2-4,(x≤-2);解得x-1=-$\sqrt{y+4}$,y≥5.把x与y互换可得:y=1+$\sqrt{x+4}$,∴圆满函数的反函数是:y=1+$\sqrt{x+4}$ (x≥5).
(2)∵x≥1,∴2x≥2,由y=$\frac{{2}^{x}}{1+{2}^{x}}$∈$[\frac{4}{5},1)$,解得:2x=$\frac{y}{1-y}$,即x=$lo{g}_{2}\frac{y}{1-y}$,把x与y互换可得原函数的反函数:y=$lo{g}_{2}\frac{x}{1-x}$,x∈$[\frac{4}{5},1)$.
(3)由y=1-3log5(x2+1)(x≥3),解得:x=$\sqrt{{5}^{\frac{1-y}{3}}-1}$,把x与y互换可得原函数的反函数:y=$\sqrt{{5}^{\frac{1-x}{3}}-1}$(x≤1-3log510).
(4)由$\frac{2-x}{2+x}$>0,解得-2<x<2.由y=log3$\frac{2-x}{2+x}$,化为:$\frac{2-x}{2+x}$=3y,解得x=$\frac{2-2•{3}^{y}}{1+{3}^{y}}$,把x与y互换可得原函数的反函数:y=$\frac{2-2•{3}^{x}}{1+{3}^{x}}$,x∈R.
(5)∵x∈(-∞,1),∴$\frac{4}{2-x}$∈(0,4),∴y=log${\;}_{\frac{1}{2}}$$\frac{4}{2-x}$∈(-2,+∞),由y=log${\;}_{\frac{1}{2}}$$\frac{4}{2-x}$,解得:x=2-2y+2,把x与y互换可得原函数的反函数:y=2-2x+2,x∈(-2,+∞).
点评 本题考查了函数的反函数的求法、方程的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3≤t≤0 | B. | -3≤t≤1 | C. | -2≤t≤0 | D. | 0≤t≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在平面α,使得a?α且b⊥α | |
| B. | 存在平面β,使得b?β 且a∥β | |
| C. | 若点A,B分别在直线a,b上,且满足AB⊥b,则一定有AB⊥a | |
| D. | 过空间某点不一定存在与直线a,b都平行的平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
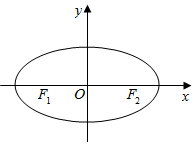 已知F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(1,0),点P(1,$\frac{\sqrt{2}}{2}$)在椭圆C上,O为坐标原点.
已知F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(1,0),点P(1,$\frac{\sqrt{2}}{2}$)在椭圆C上,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com