【答案】
分析:化简f(x)的解析式,利用已知条件中的不等式恒成立,得f(
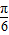
) 是三角函数的最大值,得到x=
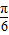
是三角函数的对称轴,由此可求出辅助角θ,再通过整体处理的思想研究函数的性质,对选项逐个判断.
解答:解:f(x)=2asinxcosx+2bcos
2x-b=asin2x+bcos2x
=
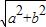
sin(2x+θ),其中tanθ=
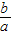
,所以周期T=π,
又f(x)≤f(
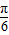
)对一切x∈R恒成立,
故x=
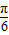
处为最大值点,即x=
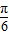
为函数图象的对称轴,
故2×
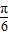
+θ=kπ+
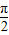
,解得θ=kπ+
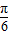
,k∈Z,
故f(x)=
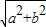
sin(2x+kπ+
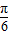
)=±
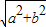
sin(2x+
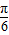
),
又x=
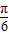
处为最大值点,故f(x)=
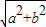
sin(2x+
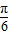
),
故①f(-
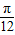
)=)=
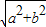
sin0=0,故正确;
②由2x+
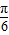
=kπ,可得x=
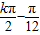
,k∈Z,当k=1时,x=
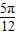
,故图象关于点(
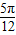
,0)对称,故正确;
③由2x+
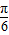
=kπ
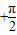
,可得x=
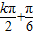
,k∈Z,令
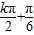
=
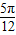
,解得k=

∉Z,故
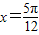
不是对称轴,故错误;
④由2kπ-

≤2x+
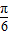
≤2kπ+
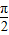
,解得kπ-
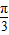
≤x≤kπ+
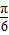
,故的函数的增区间为[kπ
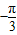
,kπ+
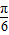
](k∈Z),故错误;
⑤函数f(x)=
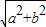
sin(2x+
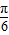
)=
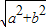
cos(
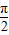
-2x-
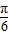
)=
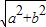
cos(
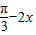
)=
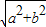
cos(2x-
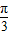
),故函数f(x)与
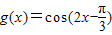
的单调区间相同,故正确.
故答案为:①②⑤
点评:本题考查三角函数的对称轴过三角函数的最值点、考查研究三角函数的性质常用整体处理的思想方法,属中档题.

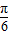 )对一切x∈R恒成立,给出下列结论:
)对一切x∈R恒成立,给出下列结论: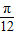 )=0; ②f(x)的图象关于点(
)=0; ②f(x)的图象关于点(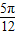 ,0)对称;
,0)对称;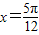 对称;
对称;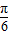 ,kπ+
,kπ+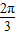 ](k∈Z);
](k∈Z);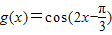 的单调区间相同.
的单调区间相同.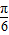 ) 是三角函数的最大值,得到x=
) 是三角函数的最大值,得到x=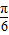 是三角函数的对称轴,由此可求出辅助角θ,再通过整体处理的思想研究函数的性质,对选项逐个判断.
是三角函数的对称轴,由此可求出辅助角θ,再通过整体处理的思想研究函数的性质,对选项逐个判断.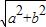 sin(2x+θ),其中tanθ=
sin(2x+θ),其中tanθ=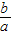 ,所以周期T=π,
,所以周期T=π,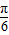 )对一切x∈R恒成立,
)对一切x∈R恒成立,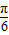 处为最大值点,即x=
处为最大值点,即x=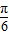 为函数图象的对称轴,
为函数图象的对称轴,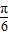 +θ=kπ+
+θ=kπ+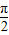 ,解得θ=kπ+
,解得θ=kπ+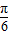 ,k∈Z,
,k∈Z,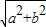 sin(2x+kπ+
sin(2x+kπ+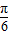 )=±
)=±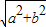 sin(2x+
sin(2x+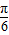 ),
),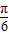 处为最大值点,故f(x)=
处为最大值点,故f(x)=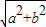 sin(2x+
sin(2x+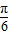 ),
),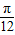 )=)=
)=)=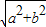 sin0=0,故正确;
sin0=0,故正确;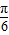 =kπ,可得x=
=kπ,可得x=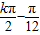 ,k∈Z,当k=1时,x=
,k∈Z,当k=1时,x=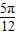 ,故图象关于点(
,故图象关于点(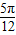 ,0)对称,故正确;
,0)对称,故正确;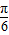 =kπ
=kπ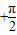 ,可得x=
,可得x=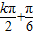 ,k∈Z,令
,k∈Z,令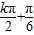 =
=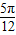 ,解得k=
,解得k= ∉Z,故
∉Z,故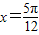 不是对称轴,故错误;
不是对称轴,故错误; ≤2x+
≤2x+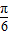 ≤2kπ+
≤2kπ+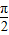 ,解得kπ-
,解得kπ-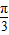 ≤x≤kπ+
≤x≤kπ+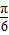 ,故的函数的增区间为[kπ
,故的函数的增区间为[kπ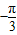 ,kπ+
,kπ+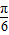 ](k∈Z),故错误;
](k∈Z),故错误;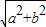 sin(2x+
sin(2x+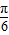 )=
)=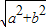 cos(
cos(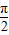 -2x-
-2x-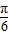 )=
)=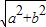 cos(
cos(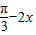 )=
)=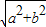 cos(2x-
cos(2x-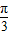 ),故函数f(x)与
),故函数f(x)与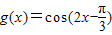 的单调区间相同,故正确.
的单调区间相同,故正确.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案