
分析 设方程x2+2mx+k=0的两实数根为α、β,方程x2+2mx+m-4=0的两实数根为e、f,则α+β=e+f=-2m,α•β=k,e•f=m-4. 再根据题意可得△=4m2-4k≥0,且α2+2mα+m-4<0,且β2+2mβ+m-4<0,化简可得m,k应满足的关系.
解答 解:设方程x2+2mx+k=0的两实数根为α、β,方程x2+2mx+m-4=0的两实数根为e、f,
则α+β=e+f=-2m,α•β=k,e•f=m-4.
若方程x2+2mx+k=0的两实数根α、β 在方程x2+2mx+m-4=0的两实数根e、f之间,
则有△=4m2-4k≥0,且α2+2mα+m-4<0,且β2+2mβ+m-4<0,
即k<m2 ①,且α2+β2+2m(α+β)+2(m-4)<0 ②.
由②可得(α+β)2-2α•β+2m(α+β)+2(m-4)<0,即 4m2-2k+2m(-2m)+2(m-4)<0,
求得k>m-4.
综上可得,m,k应满足m-4<k<m2.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
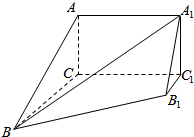 如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1
如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com