
分析 (Ⅰ)联立A与B中两函数解析式,求出解即可确定出两集合的交集;
(Ⅱ)求出A与B中y的范围确定出A与B,找出两集合的交集即可.
解答 解:(Ⅰ)联立得:$\left\{\begin{array}{l}{y={x}^{2}+2}\\{y=6-{x}^{2}}\end{array}\right.$,
消去y得:x2+2=6-x2,
解得:x=±$\sqrt{2}$,
把x=$\sqrt{2}$代入得:y=4;把x=-$\sqrt{2}$代入得:y=4,
则A∩B={($\sqrt{2}$,4),(-$\sqrt{2}$,4)};
(Ⅱ)由y=x2+2≥2,得到A={y|y≥2},
由y=6-x2≤6,得到B={y|y≤6},
则A∩B={y|2≤x≤6}.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | $\frac{31}{3}$π | C. | $\frac{32}{3}$π | D. | 11π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
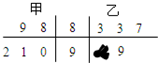 如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不低于乙的平均成绩的概率为$\frac{9}{10}$.
如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不低于乙的平均成绩的概率为$\frac{9}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com