
| A. | $\frac{43}{2}$ | B. | $\frac{55}{2}$ | C. | $\frac{125}{6}$ | D. | 22 |
分析 作出图形,则集合A∩B的所有元素组成的图形为直线与抛物线围成的封闭区域,使用定积分求出其面积.
解答 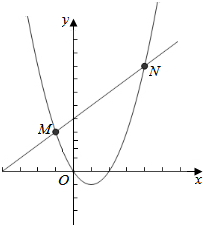 解:作出约束条件表示的平面区域如图所示,
解:作出约束条件表示的平面区域如图所示,
解方程组$\left\{\begin{array}{l}{x-y+4=0}\\{y=x(x-2)}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$.
∴M(-1.3),N(4,8).
∴直线与抛物线围成的封闭区域面积是:
${∫}_{-1}^{4}(x+4)dx$-${∫}_{-1}^{4}x(x-2)dx$=${∫}_{-1}^{4}(-{x}^{2}+3x+4)dx$=(-$\frac{{x}^{3}}{3}$+$\frac{3{x}^{2}}{2}$+4x)|$\underset{\stackrel{4}{\;}}{-1}$=$\frac{125}{6}$.
故选C.
点评 本题考查了了集合的表示法,曲边封闭图形的面积求法,作出平面区域是关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
 如图,已知AB是⊙O的一条弦,延长AB到点C使AB=BC,过点B作DB⊥AC且DB=AB,连接DA与⊙O交于点E,连接CE与⊙O交于点F.
如图,已知AB是⊙O的一条弦,延长AB到点C使AB=BC,过点B作DB⊥AC且DB=AB,连接DA与⊙O交于点E,连接CE与⊙O交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{61}$ | B. | $\sqrt{41}$ | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com