
分析 (1)解方程组$\left\{{\begin{array}{l}{2x-y-4=0}\\{x-2y+1=0}\end{array}}\right.$,得P点的坐标为(3,2).直线3x+4y-15=0斜率为 $-\frac{3}{4}$,可得垂直于直线3x+4y-15=0的直线l1的斜率为$\frac{4}{3}$,利用点斜式即可得出.
另解:垂直于直线3x+4y-15=0的直线l1的方程可设为4x-3y+C=0,又过P(3,2),代入解得C即可得出.
(2)①当所求的直线经过原点时,设方程为y=kx,又过P(3,2),代入即可得出.
②当所求的直线不经过原点时,可设方程为$\frac{x}{a}+\frac{y}{a}=1$,又过P(3,2),得a即可得出.
解答 解:(1)解方程组$\left\{{\begin{array}{l}{2x-y-4=0}\\{x-2y+1=0}\end{array}}\right.$,得P点的坐标为(3,2)…(2分)
直线3x+4y-15=0斜率为 $-\frac{3}{4}$,
则垂直于直线3x+4y-15=0的直线l1的斜率为 $\frac{4}{3}$,…(4分)
所以直线l1的方程,$y-2=\frac{4}{3}(x-3)$即4x-3y-6=0.
另解:垂直于直线3x+4y-15=0的直线l1的方程可设为4x-3y+C=0,…(4分)
又过P(3,2),∴12-6+C=0,解得C=-6.
所以直线l1的方程为:4x-3y-6=0.…(6分)
(2)①当所求的直线经过原点时,设方程为y=kx,又过P(3,2),所以直线l2的方程为2x-3y=0….…(8分)
②当所求的直线不经过原点时,可设方程为$\frac{x}{a}+\frac{y}{a}=1$,又过P(3,2),得a=5,
所以直线l2的方程为x+y-5=0….(11分)
综上所述,所求的直线l2的方程为2x-3y=0或x+y-5=0….(12分)
点评 本题考查了垂直的充要条件、直线的交点、截距式,考查了分类讨论方法、推理能力与计算能力,属于基础题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
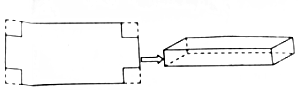 如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.
如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+x-1≥0 | B. | ?x∈R,x2+x-1<0 | ||
| C. | ?x0∈R,x02+x0-1≥0 | D. | ?x0∈R,x02+x0-1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {2} | C. | {3,4} | D. | {1,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com