
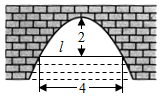
 图中是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,
图中是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,分析 根据抛物线开口向下,建立直角坐标系如图所示.设抛物线标准方程为x2=-2py(p>0),结合题意将点(2,-2)坐标代入解出p=1,从而得到该拱桥所在抛物线的标准方程,水面下降0.42米,纵坐标y=-2.42,代入方程,即可得出结论.
解答 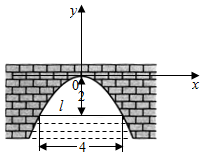 解:以抛物线的轴为y轴,抛物线的顶点为原点,建立如图所求直角坐标系
解:以抛物线的轴为y轴,抛物线的顶点为原点,建立如图所求直角坐标系
设抛物线的标准方程为x2=-2py(p>0)
∵抛物线经过点(2,-2)
∴22=-2p•2,得p=1,
即所求抛物线的标准方程为x2=-2y;
水面下降0.42米,纵坐标y=-2.42,
由x2=4.84得x=2.2,
∴水面宽为4.4m.
故答案为:4.4.
点评 本题以抛物线形拱桥为例,求曲线的方程,着重考查了抛物线的定义、标准方程与简单几何性质等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{{e}^{3}}$) | B. | ($\frac{1}{{e}^{3}}$,+∞) | C. | (-∞,$\frac{1}{3e}$) | D. | ($\frac{1}{3e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1] | C. | [0,3] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2}$ | B. | 2015 | C. | 2016 | D. | 2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com