D
����������ֱ�߷������ֱ�������������ϵĽؾ࣬�ٹ�����б��kΪ�Ա�����S
���DZ���k�ĺ��������þ�ֵ����ʽ������Сֵ��������k��0��k��0����������۴���ֱ�ߵ��������ٷ�����⣮
��𣺡�ֱ��y=k��x-2��+3��x�ᣬy�ύ�������ֱ��ǣ�A��2-
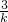
��0����B��0��3-2k����
S
��=

��|2-
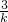
|��|3-2k|=

��

��
��k��0ʱ��S
��=

��
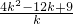
=

����4k+
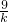
-12����
��4k+
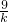
��2
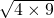
=12�����ҽ���k=

ʱȡ�Ⱥţ�
�൱S
��=m��0ʱ����k��0ʱ��k����ֵ��
��k��0ʱ��S
��=

��

=

��
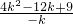
=

��[��-4k+
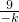
��+12]��
��-4k+
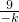
��2
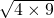
=12�����ҽ���k=-

ʱȡ�Ⱥţ�
��m��12ʱ����k��0ʱ��k����ֵ����
�൱ m=0ʱ������һ��ֱ��ʹ��AOB�����Ϊm����ٲ���ȷ��
��0��m��12ʱ����������ֱ��ʹ��AOB�����Ϊm�������ȷ��
��m=12ʱ����������ֱ��ʹ��AOB�����Ϊm�������ȷ��
��m��12ʱ����������ֱ��ʹ��AOB�����Ϊm�������ȷ��
��ѡD
��������������������������ж�������ֱ����������Χ�ɵġ���������⣮S
��������ɸ���ֱ�����������ϵĽؾ���ã��ڱ����и���б��kȡֵ�ĸ�����ȷ��ֱ�ߴ��ڵ����������ǽ��������ij��÷�����

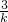 ��0����B��0��3-2k����
��0����B��0��3-2k���� ��|2-
��|2-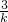 |��|3-2k|=
|��|3-2k|= ��
�� ��
�� ��
��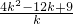 =
= ����4k+
����4k+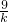 -12����
-12����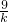 ��2
��2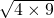 =12�����ҽ���k=
=12�����ҽ���k= ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ� ��
�� =
= ��
��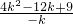 =
= ��[��-4k+
��[��-4k+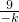 ��+12]��
��+12]��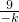 ��2
��2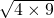 =12�����ҽ���k=-
=12�����ҽ���k=- ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮
��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮