已知x∈R，且|x|≠1，则x6＋1与x4＋x2的大小关系是________．
科目：高中数学 来源： 题型：
已知数列{an}的各项均为正数，对任意n∈N*，它的前n项和Sn满足Sn＝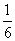
(an＋1)(an＋2)，并且a2，a4，a9成等比数列．
(1)求数列{an}的通项公式；
(2)设bn＝(－1)n＋1anan＋1，Tn为数列{bn}的前n项和，求T2n.
查看答案和解析>>
科目：高中数学 来源： 题型：
数列{an}中，a1＝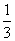
，前n项和Sn满足Sn＋1－Sn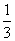＝()n＋1(n∈N*)．
(1)求数列{an}的通项公式an以及前n项和Sn；
(2)若S1，t(S1＋S2)，3(S2＋S3)成等差数列，求实数t的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知不等式ax2－bx－1≥0的解是[－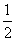
，－
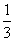]，则不等式x2－bx－a<0的解是( )
A．(2,3) B．(－∞，2)∪(3，＋∞)
C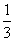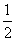．(，) D．(－∞，)∪(，＋∞)
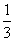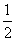查看答案和解析>>
科目：高中数学 来源： 题型：
某商店预备在一个月内分批购买每张价值为20元的书桌共36台，每批都购入x台(x是正整数)，且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费．
(1)求该月需用去的运费和保管费的总费用f(x)；
(2)能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
如右图所示，函数y＝2cos(ωx＋θ)(x∈R，ω>0,0≤θ≤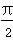
)的图象与y轴交于点(0，
)，且该函数的最小正周期为π.
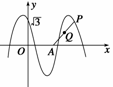
(1)求θ和ω的值；
(2)已知点A(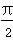，0)，点P是该函数图象上一点，点Q(x0，y0)是PA的中点，当y0＝
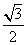，x0∈[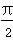，π]时，求x0的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是椭圆
(
＞
＞0)的左、右焦点，若在椭圆上存在点
,则椭圆的离心率的取值范围为 （ ）
B．
C．
D. 
的值域．
则目标函数z＝4x＋2y的最大值为( )