
已知A(1,1)是椭圆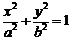 (
( )上一点,F1,F2是椭圆上的两焦点,且满足
)上一点,F1,F2是椭圆上的两焦点,且满足 。
。
(I)求椭圆方程;
(II)设C,D是椭圆上任意两点,且直线AC,AD的斜率分别为 ,若存在常数
,若存在常数 使
使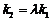 ,求直线CD的斜率。
,求直线CD的斜率。
(I) 所求椭圆方程
所求椭圆方程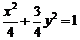 。………7分
。………7分
(II)设直线AC的方程: ,由
,由 ,得
,得
点C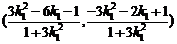 ,
,
同理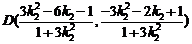
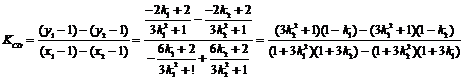
 ,
,
要使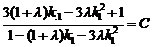 为常数,
为常数,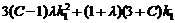 +(1-C)=0,
+(1-C)=0,
得C=1,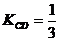 ………15分
………15分
备用:
已知点 (
( ),过点P作抛物线C:
),过点P作抛物线C: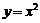 的切线,切点分别为
的切线,切点分别为 、
、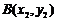 (其中
(其中 ).
).
(Ⅰ)求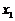 与
与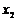 的值(用a表示);
的值(用a表示);
(Ⅱ)若以点P为圆心的圆E与直线AB相切,求圆E面积的最小值.
解:(Ⅰ)由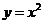 可得,
可得, .
.
∵直线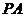 与曲线
与曲线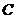 相切,且过点
相切,且过点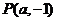 ,
,
∴ ,即
,即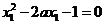 ,
,
∴ ,或
,或 ,
,
同理可得: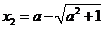 ,或
,或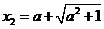
∵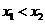 ,∴
,∴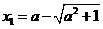 ,
,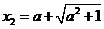 .
……6分
.
……6分
(Ⅱ)由(Ⅰ)可知,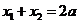 ,
,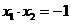 ,
,
则直线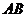 的斜率
的斜率 ,
,
∴直线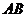 的方程为:
的方程为: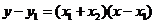 ,又
,又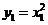 ,
,
∴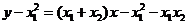 ,即
,即 .
.
∵点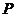 到直线
到直线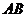 的距离即为圆
的距离即为圆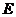 的半径,即
的半径,即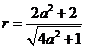 ,
,
∴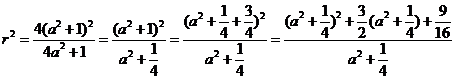
 ,
,
当且仅当 ,即
,即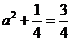 ,
,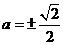 时取等号.
时取等号.
故圆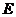 面积的最小值
面积的最小值 .
……15分
.
……15分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| x0 |
| a |
| y0 |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省怀化市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
下图展示了一个由区间 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 中的实数
中的实数 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点 ,则与实数
,则与实数 对应的实数就是
对应的实数就是 ,记作
,记作 ,
,

现给出下列5个命题
① ;
②函数
;
②函数 是奇函数;③函数
是奇函数;③函数 在
在 上单调递增; ④.函数
上单调递增; ④.函数 的图象关于点
的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
A.①③⑤ B.②③④ C.②③⑤ D.③④⑤
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二上学期期末文科数学试题(解析版) 题型:解答题
(本小题满分12分)已知A,B两点是椭圆 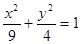 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点.
(1)设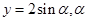 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;
(2)在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大,并求此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
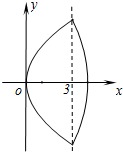 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: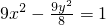 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;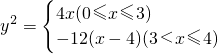 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 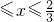 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: (
(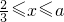 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com