
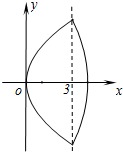 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: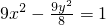 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;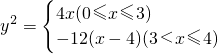 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 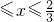 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: (
(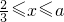 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.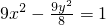 有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3,
有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3, ;
; =|x+1|,
=|x+1|, =|7-x|,
=|7-x|,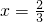 时,
时,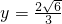 ,此时r=
,此时r= ,cosα=-
,cosα=- ;
; ≤cosα≤1时,A在椭圆弧E2上,
≤cosα≤1时,A在椭圆弧E2上,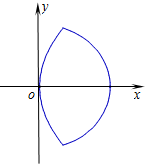
 得,3(1+r1cosα)2+4
得,3(1+r1cosα)2+4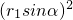 -12=0,
-12=0,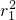 +6r1cosα-9=0,
+6r1cosα-9=0,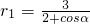 或
或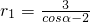 (舍去).
(舍去). 时A在抛物线弧E1上,
时A在抛物线弧E1上,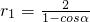 ,
,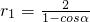 (-1
(-1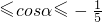 )或
)或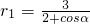 (-
(- ≤cosα≤1);
≤cosα≤1);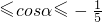 时A在抛物线弧E1上,B在椭圆弧E2上,
时A在抛物线弧E1上,B在椭圆弧E2上, =
=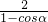
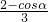 =
=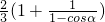 ∈[1,
∈[1, ];
];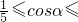 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,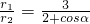 •
•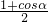 =
= ∈[
∈[ ,1];
,1];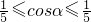 时A、B在椭圆弧E2上,
时A、B在椭圆弧E2上,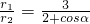
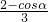 =
=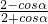 ∈(
∈( ,
, );
); 的取值范围是[
的取值范围是[ ,
, ].
].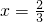 时,
时,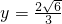 ,此时r=
,此时r= ,cosα=-
,cosα=- ,分类讨论:-
,分类讨论:- ≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤-
≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤- 时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1
时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1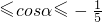 时A在抛物线弧E1上,B在椭圆弧E2上,当
时A在抛物线弧E1上,B在椭圆弧E2上,当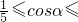 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,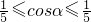 时A、B在椭圆弧E2上,利用三角函数性质分别求出
时A、B在椭圆弧E2上,利用三角函数性质分别求出 的范围即可.
的范围即可.

科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 9y2 |
| 8 |
|
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| r1 |
| r2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 和圆
和圆![]() ,且圆C与x轴交于A1,A2两点 (1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点
,且圆C与x轴交于A1,A2两点 (1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点![]() 在直线
在直线![]() 上,若存在点
上,若存在点![]() ,使得
,使得![]() (O为坐标原点),求
(O为坐标原点),求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 和圆
和圆![]() ,且圆C与x轴交于A1,A2两点
,且圆C与x轴交于A1,A2两点
(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。
(2)设点![]() 在直线
在直线![]() 上,若存在点
上,若存在点![]() ,使得
,使得![]() (O为坐标原点),求
(O为坐标原点),求![]() 的取值范围。来源:学+科+网Z+X+X+K]
的取值范围。来源:学+科+网Z+X+X+K]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com