练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    是否存在实数a，使函数f(x)＝x2－2ax＋a的定义域为[－1,1]时，值域为[－2,2]？

    若存在，求a的值；若不存在，说明理由．


    解　f(x)＝(x－a)2＋a－a2.

    当a<－1时，f(x)在[－1,1]上为增函数，

    当a>1时，f(x)在[－1,1]上为减函数，

    ∴⇒a不存在．

    综上可得a＝－1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知集合A＝{x|x≤1}，B＝{x|x≥a}，且A∪B＝R，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年

    产量x(吨)之间的函数关系式可以近似地表示为y＝－48x＋8 000，已知此生产线年产量最大为210吨．

    (1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

    (2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    (1)m为何值时，f(x)＝x2＋2mx＋3m＋4.

    ①有且仅有一个零点；②有两个零点且均比－1大；

    (2)若函数f(x)＝|4x－x2|＋a有4个零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于函数y＝x2，y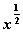＝有下列说法：

    ①两个函数都是幂函数；

    ②两个函数在第一象限内都单调递增；

    ③它们的图象关于直线y＝x对称；

    ④两个函数都是偶函数；

    ⑤两个函数都经过点(0,0)、(1,1)；

    ⑥两个函数的图象都是抛物线型．

    其中正确的有__________．(填序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝，若a≠b，且f(a)＝f(b)，则a＋b的取值范围是

    __________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝alog2x－blog3x＋2，若f＝4，则f(2 011)的值为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知对任意x∈R，不等式恒成立，求实数m的取值

    范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


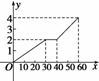
    甲同学家到乙同学家的途中有一公园，甲从家到公园的距离

    与乙从家到公园的距离都是2 km，甲10时出发前往乙家．如图所示，表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系．试写出y＝f(x)的函数解析式．

    查看答案和解析>>

    同步练习册答案