
(1)m为何值时,f(x)=x2+2mx+3m+4.
①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
解 (1)①f(x)=x2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根⇔Δ=
0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②方法一 设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
由题意,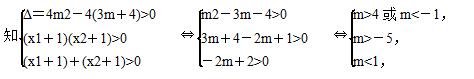
∴-5<m<-1.故m的 取值范围为(-5,-1).
取值范围为(-5,-1).
方法二 由题意,知
∴-5<m<-1.∴ m的取值范围为(-5,-1).
m的取值范围为(-5,-1).
 (2)令f(x)=0,得|4x-x2|+a=0,即|4x-x2|=-a.
(2)令f(x)=0,得|4x-x2|+a=0,即|4x-x2|=-a.
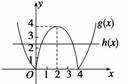
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,
即-4<a<0时,g(x)与h(x)的图象 有4个交点,即f(x)有
有4个交点,即f(x)有 4个零点.故a的取值范围为(-4,0).
4个零点.故a的取值范围为(-4,0).


科目:高中数学 来源: 题型:
某化工厂引进一条先进生产线生产某种化工产品 ,其生产的总成本y(万元)与年
,其生产的总成本y(万元)与年
产量x(吨)之间的函数关系式可以近似地表示为y=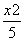 -48x+8 000,已知此生产线年产量最大为210吨.
-48x+8 000,已知此生产线年产量最大为210吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
下列结论:
①若命题p:∃ x∈R,tan x=1;命题q:∀x∈R,x2-x+1>0.则命题“p∧綈q”是假
x∈R,tan x=1;命题q:∀x∈R,x2-x+1>0.则命题“p∧綈q”是假
命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是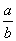 =-3;
=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.其中正确结论的序号为________.(把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com