练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲同学家到乙同学家的途中有一公园，甲从家到公园的距离

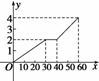
    与乙从家到公园的距离都是2 km，甲10时出发前往乙家．如图所示，表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系．试写出y＝f(x)的函数解析式．


    解　当x∈[0,30]时，设y＝k1x＋b1，

    由已知得

    当x∈(30,40)时，y＝2；

    当x∈[40,60]时，设y＝k2x＋b2，

    由已知得，

    ∴y＝x－2.

    综上，f(x)＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    是否存在实数a，使函数f(x)＝x2－2ax＋a的定义域为[－1,1]时，值域为[－2,2]？

    若存在，求a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)对一切x，y∈R，都有f(x＋y)＝f(x)＋f(y)．

    (1)求证：f(x)是奇函数；

    (2)若f(－3)＝a，用a表示f(12)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝lg(x＋3)的定义域为M，g(x)＝的定义域为N，则M∩N＝__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝若f(f(0))＝4a，则实数a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若复数满足则             ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列中，，且（，），则这个数列的通项公式               ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经统计，在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下：

    排队人数

    0

    1

    2

    3

    4

    ≥5

    概率

    0.1

    0.16

    0.3

    0.3

    0.1

    0.04

    则该营业窗口上午9点钟时，至少有2人排队的概率是      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a为实常数，y=f(x)是定义在(－∞，0)∪(0，+∞)上的奇函数，且当x<0时，f(x)=2x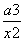－+1．

    （1）求函数f(x)的单调区间；

    （2）若f(x)≥a－1对一切x＞0成立，求a的取值范围．

    查看答案和解析>>

    同步练习册答案