
已知a为实常数,y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,f(x)=2x-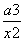 +1.
+1.
(1)求函数f(x)的单调区间;
(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.
已知a为实常数,y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,f(x)=2x-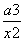 +1.(1)求函数f(x)的单调区间;(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.
+1.(1)求函数f(x)的单调区间;(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.
(1)解:由奇函数的对称性可知,我们只要讨论f(x)在区间(-∞,0)的单调性即可.
f ′(x)=2+ ,令f ′(x)=0,得x=-a. ………………………2分
,令f ′(x)=0,得x=-a. ………………………2分
①当a≤0时,f ′(x)>0,故f(x)在区间(-∞,0)是单调递增. ……………………… 4分
②当a>0时,x ∈(-∞,-a ),f ′(x)>0,所以f(x)在区间(-∞,-a )是单调递增.
x ∈(-a,0),f ′(x)<0,所以f(x)在区间(-a,0)是单调减.……………………… 6分
综上所述:当a≤0时,f(x)单调增区间为(-∞,0),(0,+∞);当a>0时,f(x)单调增区间为(-∞,-a ),(a ,+∞),单调减区间为(-a,0),(0,a).
(2)解:因为f(x)为奇函数,所以当x>0时,f(x)=-f(-x)=-(-2 x-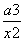 +1)=2x+
+1)=2x+ 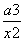 -1.… 9分
-1.… 9分
①当a<0时,要使f(x)≥a-1对一切x>0成立,即2x+ 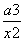 ≥a对一切x>0成立.
≥a对一切x>0成立.
而当x=-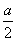 >0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.所以a<0不成立. ②当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.
>0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.所以a<0不成立. ②当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.
③当a>0时,由(1)可知f(x)在(0,a)是减函数,在(a ,+∞)是增函数.
所以fmin(x)=f(a)=3a-1>a-1,所以a>0时也满足题设要求.
综上所述,a的取值范围是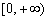 .
.


科目:高中数学 来源: 题型:
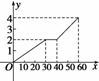
甲同学家到乙同学家的途中有一公园,甲从家到公园的距离
与乙从家到公园的距离都是2 km,甲10时出发前往乙家.如图所示,表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系.试写出y=f(x)的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,t为正实数,函数f(x)=x2-2x+a,且对任意的x∈[0,t],都有f(x)∈[-a,a].若对每一个正实数a,记t的最大值为g(a),则函数g(a)的值域为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com