
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.
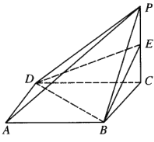
(Ⅰ)求证:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,然后利用中位线定理和线面平行的判定定理证明即可;
,然后利用中位线定理和线面平行的判定定理证明即可;
(Ⅱ)建立如图所示空间直角坐标系,先求出![]() 点坐标,求出直线
点坐标,求出直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,然后利用空间向量的夹角公式求解.
的法向量,然后利用空间向量的夹角公式求解.
解:(Ⅰ)证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
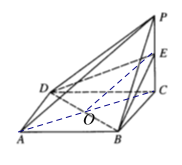
(Ⅱ)建立如图所示的空间直角坐标系,
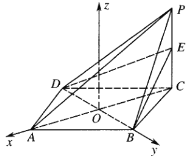
则易知![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由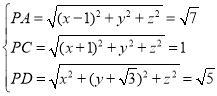 ,解得
,解得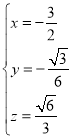 ,即
,即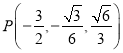 ,
,
则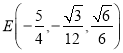 ,
,
则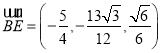 ,
,
因为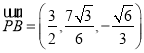 ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则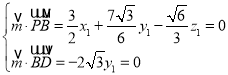 ,取
,取![]() ,则
,则![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则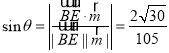 .
.
【名师指导】
本题考查空间中直线与平面的平行关系、直线与平面所成角、空间法向量的应用.求空间角,常常建立空间直角坐标系,用空间向量法计算,可减少逻辑思维量,但对计算能力要求较高.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
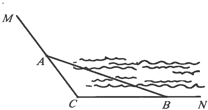
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一种水上闯关游戏,共设有3个关口,如果在规定的时间内闯过了这3个关口,那么闯关成功,否则闯关失败,结束游戏.假定小张、小王、小李闯过任何一个关口的概率分别为![]() ,且各关口能否顺利闯过相互独立.
,且各关口能否顺利闯过相互独立.
(1)求小张、小王、小李分别闯关成功的概率;
(2)记小张、小王、小李三人中闯关成功的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于![]() 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直角梯形
,直角梯形![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com