Question

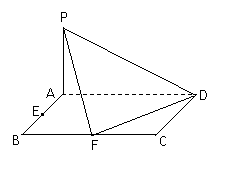
已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,

PA⊥平面ABCD.

(1)求证:PF⊥FD；w.w.w.k.s.5.u.c.o.m    

(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.

 

Answer 1

解析：（1）证明:连结AF,在矩形ABCD中,因为AD=4,AB=2,点F是BC的中点,

所以∠AFB=∠DFC=45°. w.w.w.k.s.5.u.c.o.m    

所以∠AFD=90°,即AF⊥FD. ………3分

又PA⊥平面ABCD,所以PA⊥FD.… 4分

所以FD⊥平面PAF. ……………  5分

故PF⊥FD. ………………………6分

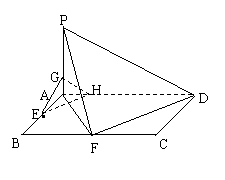
(2)过E作EH//FD交AD于H,则EH//平面PFD,

且AH=AD.         …………………………8分

再过H作HG//PD交PA于G,则GH//平面PFD,且 AG=PA. ………………10分

所以平面EHG//平面PFD,则EG//平面PFD, …………………………12分

从而点G满足AG=PA. 即点的位置为上靠近的四等分点处…………14分

[说明:①用向量法求解的,参照上述评分标准给分；②第(2)小题也可以延长DF与AB交于R,然后找EG//PR进行处理.]