
(本小题满分14分)已知椭圆C :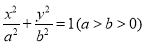 , 经过点P
, 经过点P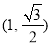 ,离心率是
,离心率是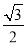 .
.
(1)求椭圆C的方程;
(2)设直线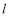 与椭圆
与椭圆 交于
交于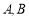 两点,且以
两点,且以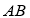 为直径的圆过椭圆右顶点
为直径的圆过椭圆右顶点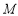 ,求证:直线l恒过定点.
,求证:直线l恒过定点.
(1)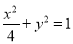 ; (2)详见解析;
; (2)详见解析;
【解析】
试题分析:(1)由椭圆过点P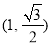 得
得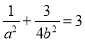 ,由离心率是
,由离心率是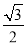 得
得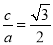 ,另外结合
,另外结合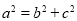 列方程组即可确定
列方程组即可确定 的值从而得到椭圆C的方程;
的值从而得到椭圆C的方程;
(2)设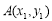 ,
,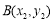 ,直线
,直线 的方程为
的方程为 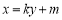 ,或
,或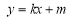 ,将直线方程与椭圆方程联立消去一个变量,得到关于
,将直线方程与椭圆方程联立消去一个变量,得到关于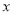 或
或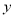 的一元二次方程,结合一元二次方程根的判别式与韦达定理以及平面向量的数量积
的一元二次方程,结合一元二次方程根的判别式与韦达定理以及平面向量的数量积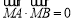 确定的关系,从而找出定点坐标.注意不论直线的方程设为哪一种形式都要先考察它与坐标轴平行的特殊情况.
确定的关系,从而找出定点坐标.注意不论直线的方程设为哪一种形式都要先考察它与坐标轴平行的特殊情况.
试题解析:【解析】
(1)由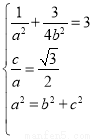 ,解得
,解得 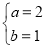 ,
,
所以椭圆C的方程是 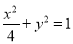 . . 5分
. . 5分
(2)方法一
(1)由题意可知,直线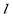 的斜率为0时,不合题意.
的斜率为0时,不合题意.
(2)不妨设直线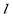 的方程为
的方程为 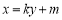 .
.
由 消去
消去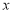 得
得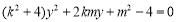 . 7分
. 7分
设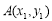 ,
,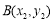 ,则有
,则有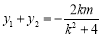 ①,
①, 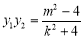 ② 8分
② 8分
因为以 为直径的圆过点
为直径的圆过点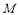 ,所以
,所以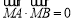 .
.
由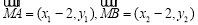 ,得
,得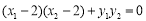 .
.
将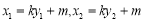 代入上式,
代入上式,
得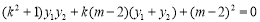 . ③ 12分
. ③ 12分
将①②代入③,得 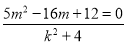 ,
,
解得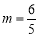 或
或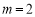 (舍).
(舍).
综上,直线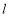 经过定点
经过定点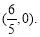 14分
14分
方法二
证明:
(1)当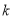 不存在时,易得此直线恒过点
不存在时,易得此直线恒过点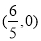 . 7分
. 7分
(2)当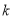 存在时.设直线
存在时.设直线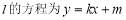 ,,
,,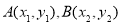 ,
,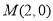 .
.
由 ,可得
,可得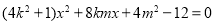 .
.
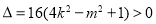
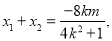 ①
①
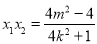 .② 9分
.② 9分
由题意可知
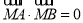 ,
,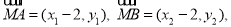
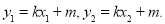
可得 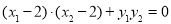 . 10分
. 10分
整理得 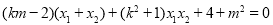 ③
③
把①②代入③整理得 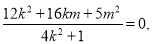
由题意可知 
解得 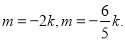
(1)当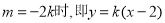 ,直线过定点(2,0)不符合题意,舍掉. 12分
,直线过定点(2,0)不符合题意,舍掉. 12分
(2)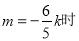 ,即
,即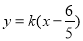 ,直线过定点
,直线过定点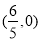 ,经检验符合题意.
,经检验符合题意.
综上所述,直线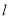 过定点
过定点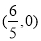 14分
14分
考点:1、椭圆的标准方程与简单几何性质;2、直线与圆锥曲线的位置关系综合问题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)函数 部分图象如图所示.
部分图象如图所示.
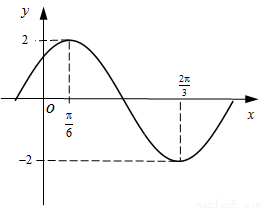
(Ⅰ)求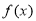 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设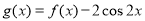 ,求函数
,求函数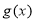 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测文科数学试卷(解析版) 题型:选择题
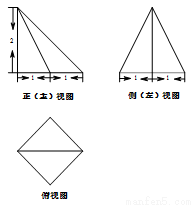
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是
A. B.
B.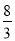 C.
C.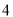 D.
D.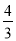
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测理科数学试卷(解析版) 题型:填空题
已知函数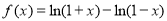 ,有如下结论:
,有如下结论:
①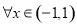 ,有
,有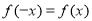 ;②
;②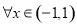 ,有
,有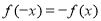 ;
;
③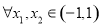 ,有
,有 ;
;
④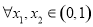 ,有
,有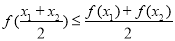 .
.
其中正确结论的序号是 .(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测理科数学试卷(解析版) 题型:选择题
在 中,角
中,角 对应的边分别为
对应的边分别为 .若
.若 则“
则“ ”是“
”是“ ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高一上学期一模数学试卷(解析版) 题型:选择题
若函数 满足
满足 ,则称为满足“倒负”变换的函数,下列函数:
,则称为满足“倒负”变换的函数,下列函数:
① ;②
;② ;③
;③ 其中满足“倒负”变换的函数是 ( )
其中满足“倒负”变换的函数是 ( )
A.①② B.①③ C.②③ D.①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com