
分析 因为命题“p∨q”为真命题,且“p∧q”为假命题,所以p,q一真一假,进而得到答案.
解答 解:∵m∈[-1,1],
∴$\sqrt{{m^2}+8}$∈[2$\sqrt{2}$,3],
若不等式a2-5a-3≥$\sqrt{{m^2}+8}$恒成立,
则a2-5a-3≥3,
则a≤-1,或a≥6,
因为函数f(x)=lg(x2-4x+a2)的定义域为R
,所以x2-4x+a2>0恒成立,
即△=16-4a2<0,解得a<-2或a>2.
因为命题“p∨q”为真命题,且“p∧q”为假命题,
所以p,q一真一假,
(1)p真q假时,$\left\{\begin{array}{l}a≥6或a≤-1\\-2≤a≤2\end{array}\right.$,解得-2≤a≤-1;
(2)$\begin{array}{l}p假q真时\end{array}$,$\left\{\begin{array}{l}-1<a<6\\ a<-2或a>2\end{array}\right.$,解得2<a<6.
综上所述:a的取值范围为[-2,-1]∪(2,6)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的单调性,二次方程根的个数判断等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{{\sqrt{2}}}{2},0$] | B. | [-1,0] | C. | [-$\sqrt{2},0$] | D. | [-$\sqrt{3},0$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
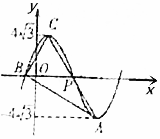 已知函数f(x)=4$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在平面直角坐标系中的部分图象如图所示,若∠ABC=90°,则ω=( )
已知函数f(x)=4$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在平面直角坐标系中的部分图象如图所示,若∠ABC=90°,则ω=( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
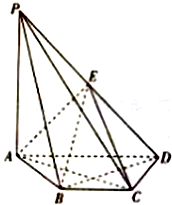 如图所示,在四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,E为PD中点,PA⊥平面ABCD,AD∥BC,AC⊥BD,AD=2BC=4.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,E为PD中点,PA⊥平面ABCD,AD∥BC,AC⊥BD,AD=2BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos(2x-$\frac{π}{10}$) | B. | y=cos(2x-$\frac{π}{5}$) | C. | y=cos($\frac{1}{2}$x-$\frac{π}{10}$) | D. | y=cos($\frac{1}{2}$x-$\frac{π}{20}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com