
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
 若椭圆E1:
若椭圆E1:| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
| a2 |
| a1 |
| b2 |
| b1 |
|
| 6 |
| x2 |
| 4 |
| y2 |
| 2 |
| 1 |
| |OB| |
| x2 |
| 22 |
| y2 | ||
(
|
| x2 |
| 42 |
| y2 | ||
(2
|
| x2 |
| 32 |
| y2 | ||||
(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:013
设Sn和Tn分别是两个等差数列![]() 的前n项之和,如果对于所有的自然数n,都有
的前n项之和,如果对于所有的自然数n,都有![]() ,则
,则![]() 的值为
的值为
[
]A
.7∶4 B.4∶3 C.78∶71 D.不能确定查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求点P的轨迹方程;
(2)对于x轴上的点M,若满足![]() ,则称点M为点P对应的“比例点”,求证:对任意一个确定的点P,它总对应两个“比例点”;
,则称点M为点P对应的“比例点”,求证:对任意一个确定的点P,它总对应两个“比例点”;
(3)当点P在(1)的轨迹上运动时,求它在(2)中对应的“比例点”M的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源:2009年上海市松江区高考数学二模试卷(理科)(解析版) 题型:解答题
 和椭圆E2:
和椭圆E2: 满足
满足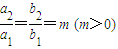 ,则称这两个椭圆相似,m称为其相似比.
,则称这两个椭圆相似,m称为其相似比. ,且与椭圆
,且与椭圆 相似的椭圆方程;
相似的椭圆方程; 的最大值和最小值;
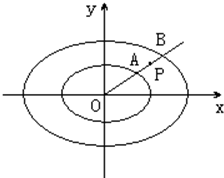
的最大值和最小值;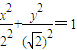 和C2:
和C2: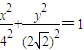 交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为 ”.请用推广或类比的方法提出类似的一个真命题,并给予证明.
”.请用推广或类比的方法提出类似的一个真命题,并给予证明.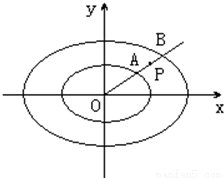
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com