
分析 由函数f(x)的定义域是(0,1],求出f(x+a)、f(x-a)的定义域,然后对a分类求解φ(x)=f(x+a)+f(x-a),(-1<a<0)的定义域.
解答 解:∵函数f(x)的定义域是(0,1],
∴由0<x+a≤1,得-a<x≤1-a,
∴f(x+a)的定义域为(-a,1-a];
由0<x-a≤1,得a<x≤1+a,
∴f(x-a)的定义域为(a,1+a].
当-1$<a≤-\frac{1}{2}$时,1+a≤-a,
取交集可得φ(x)=f(x+a)+f(x-a)的定义域为∅;
当$-\frac{1}{2}<a<0$时,-a<1+a<1-a,
取交集可得φ(x)=f(x+a)+f(x-a)的定义域为(-a,1+a].
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的解决方法,同时体现了分类讨论的数学思想方法,是中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
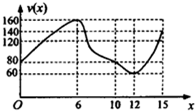 一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )
一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )| A. | 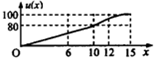 | B. | 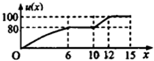 | ||
| C. | 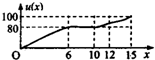 | D. | 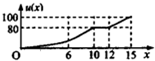 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com